Формулы конденсатора

Формулы емкости конденсаторов

Для любого конденсатора справедлива формула:

$C=\frac{q}{U}=\frac{q}{{\varphi }_1-{\varphi }_2} \qquad(1)$

где C – емкость конденсатора; q – величина заряда одной из обкладок конденсатора; $U={\varphi }_1-{\varphi }_2$ – разность потенциалов между его обкладками.

Емкость конденсатора, между пластинами которого находится диэлектрик (C) (диэлектрическая проницаемость которого равна $\varepsilon)$ в $\varepsilon$ раз больше, чем емкость такого же воздушного конденсатора ( $C_0$ ):

$C=\varepsilon C_0 \qquad(2)$

Для расчета емкости плоского конденсатора применяют формулу:

$C=\frac{\varepsilon {\varepsilon }_0S}{d} \qquad(3)$

где ${\varepsilon }_0$ – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.

Емкость плоского конденсатора, содержащего N слоев диэлектрика (толщина i-го слоя равна $d_i)$ , диэлектрическая проницаемость i-го слоя ${\varepsilon }_i$ , определяется как:

$C=\frac{{\varepsilon }_0S}{\sum^N_{i=1}{\frac{d_i}{{\varepsilon }_i}}} \qquad(4)$

Электрическая емкость цилиндрического конденсатора вычисляют как:

$C=\frac{2\pi \varepsilon {\varepsilon }_0l}{ln\left(\frac{R_2}{R_1}\right)} \qquad(5)$

где l – высота цилиндров; $R_2$ – радиус внешней обкладки; $R_1$ – радиус внутренней обкладки.

Емкость сферического (шарового) конденсатора находят по формуле:

$C=\frac{4\pi \varepsilon {\varepsilon }_0R_1R_2}{R_2-R_1} \qquad(6)$

где $R_1{;\ R}_2$ – радиусы обкладок конденсатора.

Формулы для расчета емкости соединения конденсаторов

При параллельном соединении конденсаторов суммарная емкость батареи (C) равна сумме емкостей отдельных конденсаторов ( $C_i$ ), ее составляющих:

$C=\sum{C_i} \qquad (7)$

Электрическая емкость последовательного соединения конденсаторов может быть вычислена по формуле:

$\frac{1}{C}=\sum^N_{i=1}{\frac{1}{C_i}} \qquad(8)$

Если последовательно соединены N конденсаторов, с емкостями $C_1$ то емкость батареи вычислим как:

$C=\frac{1}{N}C_1\ \qquad(9)$

Сопротивление конденсатора

При включении конденсатора в цепь с постоянным током сопротивление конденсатора считают бесконечно большим.

Если конденсатор включен в цепь переменного тока, то его сопротивление называют емкостным и вычисляют при помощи формулы:

$X_C=\frac{1}{2\pi \nu C}=\frac{1}{\omega C}\left(10\right)$

где $\nu$ – частота переменного тока; $\omega$ – угловая частота тока; C – емкость конденсатора.

Формула энергии поля конденсатора

$W_p=\frac{q\Delta \varphi }{2}=\frac{C{\left(\Delta \varphi \right)}^2}{2}=\frac{q^2}{2C}\ \left(11\right)$

где $W_p$ –энергия поля конденсатора; q – заряд конденсатора; C – емкость конденсатора; $\Delta \varphi$ – разность потенциалов между обкладками конденсатора.

Энергия поля плоского конденсатора:

$W_p=\frac{q^2}{2\varepsilon \varepsilon _0S}d=\frac{\varepsilon {\varepsilon }_0E^2}{2}Sd=\frac{\varepsilon {\varepsilon }_0E^2}{2}V\ \ \left(12\right)$

Примеры решения задач по теме «Конденсатор»

ПРИМЕР 1

Задание

Между пластинами плоского конденсатора находятся два слоя диэлектрика: стекло, толщиной $d_1=7$ мм и эбонит толщиной $d_2=3$ мм, которые вместе полностью заполняют пространство. Площади обкладок конденсатора равны S=0,02 м². Какова электрическая емкость конденсатора?

Решение

Для решения задачи применим выражение, определяющее емкость многослойного плоского конденсатора:

$C=\frac{{\varepsilon }_0S}{\sum^N_{i=1}{\frac{d_i}{{\varepsilon }_i}}} \qquad(1.1)$

где мы имеем по условию два слоя (N=2), преобразуем выражение (1.1) согласно нашим условиям:

$C=\frac{{\varepsilon }_0S}{\frac{d_1}{{\varepsilon }_1}+\frac{d_2}{{\varepsilon }_2}}\ \qquad(1.2)$

Диэлектрические проницаемости стекла и эбонита возьмем из справочников: для стекла ${\varepsilon }_1=7;$ для эбонита ${\varepsilon }_2=3.$

Подставим имеющиеся данные, произведем расчет:

$C=\frac{8,85\cdot {10}^{-12}\cdot 0,02}{\frac{7\cdot {10}^{-3}}{7}+\frac{3\cdot {10}^{-3}}{3}}=88,5\cdot {10}^{-12}(F)$

Ответ

С=88,5 пФ

ПРИМЕР 2

Задание

Конденсаторы, имеющие емкости 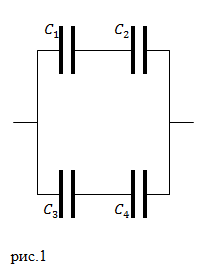$C_1$ ; $C_2$ ; $C_3$ ; $C_4$ соединены так, как показано на рис.1. Какова емкость батареи конденсаторов?

Решение

В представленной схеме мы имеем смешанное соединение конденсаторов. Конденсаторы $C_1$ и $C_2$ соединены последовательно, значит их суммарную емкость ( $C_{12}$ ) найдем как:

$C_{12}=\frac{C_1C_2}{C_1{+C}_2}\ \qquad(2.1)$