Формула дифракционной решетки

ОПРЕДЕЛЕНИЕ

Дифракционная решетка – это простейший спектральный прибор, состоящий из системы щелей (прозрачных для света участков), и непрозрачных промежутков, которые сравнимы с длиной волны.

Одномерная дифракционная решетка, состоит из параллельных щелей одинаковой ширины, которые лежат в одной плоскости, разделяемых одинаковыми по ширине непрозрачными для света промежутками. Лучшими считаются отражательные дифракционные решетки. Они состоят из совокупности участков, отражающих свет и участков, которые свет рассеивают. Данные решетки представляют собой отшлифованные металлические пластины, на которые рассеивающие свет штрихи нанесены резцом.

Картиной дифракции на решетке — является результат взаимной интерференции волн, идущих ото всех щелей. С помощью дифракционной решетки реализуется многолучевая интерференция когерентных пучков света, подвергшихся дифракции и которые идут от всех щелей.

Характеристикой дифракционной решетки служит ее период. Периодом дифракционной решетки (d) (ее постоянной) называют величину, равную:

$d=a+b\ \qquad(1)$

где a — ширина щели; b — ширина непрозрачного участка.

Дифракция на одномерной дифракционной решетке

Допустим, что перпендикулярно к плоскости дифракционной решетки падает световая волна с длиной $\lambda$ . Так как щели у решетки расположены на равных расстояниях друг от друга, то разности хода лучей ( $\Delta$ ), идущих от двух соседних щелей, для направления $\varphi$ будут одинаковы для всей рассматриваемой дифракционной решетки:

$\Delta =d{\sin \varphi } \qquad (2)$

Главные минимумы интенсивности наблюдаются в направлениях, определенных условием:

$a\sin \varphi =\pm k\lambda \ (k=1,2,3\dots )} \qquad (3)$

Кроме главных минимумов, в результате взаимной интерференции лучей света, которые идут от двух щелей, в некоторых направлениях лучи гасят друг друга. В результате возникают дополнительные минимумы интенсивности. Они появляются в тех направлениях, где разность хода лучей составляют нечетное число полуволн. Условием дополнительных минимумов является формула:

$d{\sin \varphi =\pm k'\frac{\lambda}{N}\qquad \left(k'=1,2,\dots ,N-1,N+1,\dots ,2N-1,2N+1,\dots \right)} \qquad (4)$

где N – количество щелей дифракционной решетки; $k^'$ — целые значения кроме 0, $N,\ 2N,...$ В том случае, если решетка имеет N щелей, то между двумя главными максимумами находятся $N-1$ дополнительный минимум, которые разделяют вторичные максимумы.

Условием главных максимумов для дифракционной решетки является:

$d{\sin \varphi =\pm m\lambda (m=0,1,2,\dots )} \qquad (5)$

Величина синуса не может быть больше единицы, то количество главных максимумов:

$m\le \frac{d}{\lambda } \qquad(6)$

Примеры решения задач по теме «Дифракционная решетка»

ПРИМЕР 1

Задание

На дифракционную решетку, перпендикулярно ее поверхности падает монохроматический пучок света с длиной волны 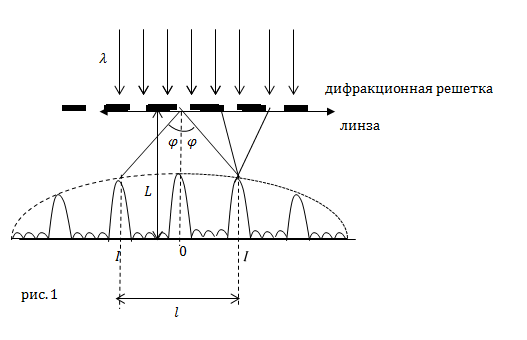$\lambda$ . На плоский экран картина дифракции проецируется при помощи линзы. Расстояние между двумя максимумами интенсивности первого порядка составляет l. Какова постоянная дифракционной решетки, если линза размещена в непосредственной близости от решетки и расстояние от нее до экрана равно L. Считайте, что $\frac{l}{2}\ll L.$

Решение

В качестве основы для решения задачи используем формулу, которая связывает постоянную дифракционной решетки, длину волны света и угол отклонения лучей, который соответствует дифракционному максимуму номер m:

$d{\sin \varphi =m\lambda (m=0,1,2,\dots )} \qquad (1.1)$

По условию задачи $m=1.$ Так как угол отклонения лучей можно считать малым ( $\frac{l}{2}\ll L$ ), то примем, что:

$tg\ \varphi \approx {\sin \varphi } \qquad(1.2)$

Из рис.1 следует, что:

$tg\ \varphi =\frac{l}{2}:L=\frac{l}{2L} \qquad(1.3)$

Подставим в формулу (1.1) выражение (1.3) и учтем, что $m=1$ , получим:

$d\frac{l}{2L}=\lambda \ \qquad(1.4)$

Из (1.4) выразим период решетки:

$d=\frac{2L\lambda }{l}$

Ответ

$d=\frac{2L\lambda }{l}$

ПРИМЕР 2

Задание

Используя условия примера 1, и результат решения, найдите количество максимумов, которое даст рассматриваемая решетка.

Решение

Для того чтобы определить максимальный угол отклонения лучей света в нашей задаче найдем число максимумов, которое может дать наша дифракционная решетка. Для этого используем формулу:

$d{\sin \varphi =m\lambda \left(m=0,1,2,\dots \right)} \qquad (2.1)$

где положим, что $m=\ m_{max}$ при ${\sin \varphi =1}$ . Тогда, получим:

$m_{max}=\frac{d}{\lambda }\ \qquad(2.2)$

Следует учесть при вычислениях, что число $m_{max}$ обязательно целое и синус угла $\varphi$ обязательно меньше единицы. При этом общее количество максимумов картины дифракции справа и слава от центрального максимума одинаково и равно: