ЭДС индукции в движущихся проводниках формула

ЭДС индукции и сила Лоренца

Появление электродвижущей силы (ЭДС) в телах, перемещающихся в магнитном поле легко объяснить, если вспомнить о существовании силы Лоренца. Пусть стержень движется в однородном магнитном поле с индукцией $\overline{B}$ рис.1. Пусть направление скорости движения стержня ( $\overline{v}$ ) и $\overline{B}$ перпендикулярны друг другу.

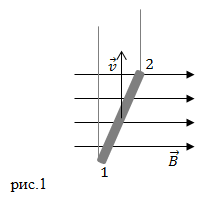
ЭДС индукции в движущихся проводниках формула, рисунок 1

Между точками 1 и 2 стержня индуцируется ЭДС, которая направлена от точки 1 к точке 2. Движение стержня – это перемещение положительных и отрицательных зарядов, которые входят в состав молекул этого тела. Заряды вместе с телом перемещаются в сторону движения стержня. Магнитное поле оказывает воздействие на заряды при помощи силы Лоренца, пытаясь переместить положительные заряды в сторону точки 2, а отрицательные заряды к противоположному концу стержня. Так, действие силы Лоренца порождает ЭДС индукции.

Если в магнитном поле движется металлический стержень, то положительные ионы, находясь в узлах кристаллической решетки, не могут двигаться вдоль стержня. При этом подвижные электроны скапливаются в избытке на конце стержня около точки 1. Противоположный конец стержня будет испытывать недостаток электронов. Появившееся напряжение $U_{12}$ определяет собой ЭДС индукции.

В том случае, если движущийся стержень сделан из диэлектрика, разделение зарядов при воздействии силы Лоренца, приводит к его поляризации.

ЭДС индукции будет равна нулю, если проводник перемещается параллельно направлению вектора $\overline{B}$ (то есть угол между $\overline{B}$ и $\overline{v}$ равен нулю).

ЭДС индукции в прямом проводнике, движущемся в магнитном поле

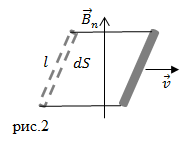
Получим формулу для вычисления ЭДС индукции, которая возникает в прямолинейном проводнике, имеющем длину l, движущемся параллельно самому себе в магнитном поле (рис.2). Пусть v – мгновенная скорость проводника, тогда за время $dt$ он опишет площадь равную:

$dS=lvdt \qquad (1)$

При этом проводник пересечет все линии магнитной индукции, которые проходят через площадку $dS$ . Получим, что изменение магнитного потока ( $d\Phi$ ) сквозь контур в который входит перемещающийся проводник:

ЭДС индукции в движущихся проводниках формула, рисунок 2

$d\Phi=B_nlvdt \qquad (2)$

где $B_n$ – составляющая магнитной индукции, перпендикулярная к площадке $dS$ . Подставим выражение для $d\Phi$ (2) в основной закон электромагнитной индукции:

$\varepsilon_i=-\frac{d\Phi}{dt} \qquad (3)$

получим:

$\varepsilon_i=-B_nlv \qquad (4)$

При этом направление тока индукции определено законом Ленца. То есть индукционный ток имеет такое направление, что механическая сила, которая действует на проводник, замедляет перемещение проводника.

ЭДС индукции в плоском витке, вращающемся в магнитном поле

Если плоский виток вращается в однородном магнитном поле, угловая скорость его вращения равна $\overline{\omega}$ , ось вращения находится в плоскости витка и $\overline{\omega}\bot \overline{B}$ , тогда ЭДС индукции можно найти как:

$\varepsilon_i=B_0S\omega {\sin \left(\omega t\right)-\frac{d\Phi_{m0}}{dt}} \qquad (5)$

где S – площадь, которую ограничивает виток; $\Phi_{m0}$ – поток самоиндукции витка; $\omega$ – угловая скорость; ( $\omega t$ ) – угол поворота контура. Необходимо заметить, что выражение (5) справедливо, тогда, когда ось вращения составляет прямой угол с направлением вектора внешнего поля $\overline{B}$ .

Если вращающаяся рамка имеет N витков и ее самоиндукцией можно пренебречь, то:

$\varepsilon_i=B_0S\omega {\sin \left(\omega t\right)} \qquad (6)$

Примеры решения задач

ПРИМЕР 1

Задание

Автомобильная антенна, расположенная вертикально движется с востока на запад в магнитном поле Земли. Длина антенны $l=2$ м, скорость перемещения составляет $v=16 \frac{m}{c}$ . Каким будет напряжение между концами проводника?

Решение

Антенна – это разомкнутый проводник, следовательно, тока в нем не будет, напряжение на концах равно ЭДС индукции:

$U=\varepsilon_i \qquad (1.1)$

Составляющая вектора магнитной индукции поля Земли, перпендикулярная направлению движения антенны для средних широт примерно равна $B_n=0,2\cdot {10}^{-4}$ Тл.

В качестве основы для решения задачи используем формулу вычисления ЭДС проводника, перемещающегося в магнитном поле Земли:

$\varepsilon_i=-B_nlv=U \qquad (1.2)$

Вычислим напряжение:

$U=0,2\cdot {10}^{-4}\cdot 2\cdot 16=6,4\cdot {10}^{-4}\ (B)$

Магнитное поле Земли имеет направление с юга на север. Получим, что ЭДС индукции направлена сверху вниз. Нижний конец антенны будет заряжен положительно, верхний конец будет нести отрицательный заряд.

Ответ

$U=6,4\cdot {10}^{-4}$ В

ПРИМЕР 2

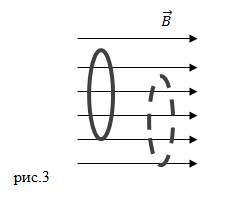
Задание

Замкнутый виток проводника перемещается поступательно в однородном магнитном поле (рис.3). Чему равна ЭДС индукции и сила индукционного тока в этом случае?

ЭДС индукции в движущихся проводниках формула, пример 1

Решение

Если замкнутый виток проводника перемещается поступательно в однородном магнитном поле, то магнитный поток через площадь этого витка при перемещении не изменяется. Тогда в соответствии основным законом электромагнитной индукции ЭДС индукции будет равна нулю:

$\varepsilon_i=-\frac{d\Phi}{dt}=0 \qquad (2.1)$

Следовательно, тока в витке также не будет. В случае, который представлен на рис.3 линии магнитной индукции пересекают отдельные части витка, в них появляется ЭДС. Но результирующая ЭДС, равная сумме ЭДС его частей, равна нулю. Для возникновения в контуре, который не изменяет свою форму и перемещается в однородном магнитном поле, возникала ЭДС, необходимо, чтобы контур поворачивался (рис.4).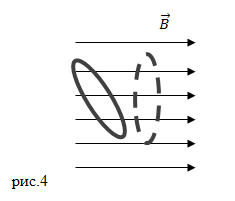

ЭДС индукции в движущихся проводниках формула, пример 2

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

ЭДС индукции в движущихся проводниках формула

ЭДС индукции и сила Лоренца

ЭДС индукции в прямом проводнике, движущемся в магнитном поле

ЭДС индукции в плоском витке, вращающемся в магнитном поле

Примеры решения задач