Формула ЭДС индукции

ОПРЕДЕЛЕНИЕ

ЭДС – это аббревиатура от электродвижущей силы индукции ( $\varepsilon_i$ .) Электромагнитная индукция возникает в проводнике, который находится в переменном магнитном поле. Если в качестве проводника выступает замкнутый проводящий контур, то в нем появляется электрический ток, который называется током индукции.

Закон Фарадея – Максвелла для электромагнитной индукции

Основной формулой, которая определяет ЭДС индукции, является закон Фарадея – Максвелла, больше известный как основной закон электромагнитной индукции (или закон Фарадея). Этот закон утверждает, что ЭДС индукции в контуре, находящемся в переменном магнитном поле, равна по величине и противоположна по знаку скорости изменения магнитного потока ( $\Psi_m$ ) через поверхность, которую ограничивает данный контур:

$\varepsilon_i=-\frac{d\Psi_m}{dt} \qquad(1)$

где $\frac{d\Psi_m}{dt}$ – скорость изменения магнитного потока. Полная производная в законе (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) соответствует правилу Ленца. Формула (1) для ЭДС индукции записана для системы СИ.

В случае равномерного изменения магнитного потока формулу ЭДС индукции можно записать как:

$\varepsilon_i=-\frac{\Delta \Psi_m}{\Delta t} \qquad(2)$

Частные случаи формул ЭДС индукции

Если контур содержит N витков, которые соединяются последовательно, то ЭДС индукции вычисляют как:

$\varepsilon_i=-\frac{d\sum^N_{i=1}{\Psi_{mi}}}{dt}=-\frac{d\Psi}{dt} \qquad(3)$

где $\Psi=N\Psi_m$ – потокосцепление.

При движении прямолинейного проводника в однородном магнитном поле в нем возникает ЭДС индукции, которая равна:

$\varepsilon_i=-vBl\ \qquad(4)$

где v – скорость движения проводника; l – длина проводника; B – модуль вектора магнитной индукции поля; $\overrightarrow{B}\bot \overrightarrow{v}$ .

При вращении с постоянной скоростью в однородном магнитном поле плоского контура вокруг оси, которая лежит в плоскости контура в нем возникает ЭДС индукции, равная:

$\varepsilon_i=B_0S\omega {\sin \left(\omega t\right)-\frac{d\Psi_{m0}}{dt}} \ \qquad(5)$

где S – площадь, которую ограничивает виток; $\Psi_{m0}$ – поток самоиндукции витка; $\omega$ — угловая скорость; ( $\omega t$ ) – угол поворота контура. Следует учесть, что формула (5) справедлива, если ось вращения составляет прямой угол с направлением вектора внешнего поля ${\overrightarrow{B}}_0$ .

Если во вращающейся рамке имеется N витков и самоиндукцией рассматриваемой системы можно пренебречь, то:

$\varepsilon_i=B_0S\omega {\sin \left(\omega t\right)} \ \qquad(6)$

В стационарном проводнике, который находится в переменном магнитном поле, ЭДС индукции находят по формуле:

$\varepsilon_i=-\frac{\partial \Psi_m}{\partial t} \qquad(7)$

Примеры решения задач по теме «ЭДС индукции»

ПРИМЕР 1

Задание

Какова электродвижущая сила магнитной индукции в соленоиде, который находится в магнитном поле, индукция которого изменяется со скоростью ${10} ^{-3}\frac{Tl}{c}$ ? Диаметр соленоида равен $d=0,04$ м, число витков в нем равно $N=500$ , ось соленоида составляет угол $\alpha =45^\circ$ с направлением вектора магнитной индукции поля.

Решение

За основу решения задачи примем закон Фарадея – Максвелла:

$\varepsilon_i=-\frac{d\Psi_m}{dt} \qquad(1.1)$

Поток магнитной индукции через N витков соленоида будет равен:

$\Psi_m=NBS{\cos \alpha } \qquad (1.2)$

где площадь ограниченная каждым витком соленоида составляет:

$S=\frac{\pi d^2}{4} \qquad(1.3)$

Далее мы будем рассматривать модуль ЭДС индукции. Подставляем выражения (1.2) и (1.3) в закон электромагнитной индукции (1.1), получаем:

$\left|\varepsilon_i\right|=\frac{d}{dt}\left(NB\frac{\pi d^2}{4}\cos \alpha \ } \right)=N\frac{\pi d^2}{4}\cos \alpha \ } \frac{dB}{dt}\ \qquad(1.4)$

где $\frac{dB}{dt}$ – скорость изменения индукции магнитного поля.

Проведем вычисления:

$\left|\varepsilon_i\right|=500\frac{3,14\cdot {(0,04)}^2}{4}\cos (45^\circ )\ \cdot } {10} ^{-3}=4,44\cdot {10} ^{-4}(B)$

Ответ

$\left|\varepsilon_i\right|=4,44\cdot {10} ^{-4}$ В

ПРИМЕР 2

Задание

Какова угловая скорость ( $\omega$ ) проводящего стержня, равномерно вращающегося в однородном магнитном поле с индукцией B? Если горизонтальный стержень совершает вращение вокруг вертикальной оси. Ось проходит через один из концов стержня, параллельно линиям магнитной индукции поля. Длина стержня l. Разность потенциалов, которая появляется на концах стержня при его вращении, равна $U.$

Решение

На рис.1 изобразим схематично то, что происходит в задаче.

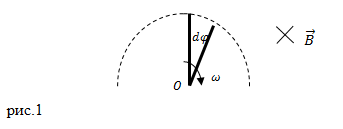
В качестве основы для решения задачи используем основной закон электромагнитной индукции (закон Фарадея – Максвелла):

$\varepsilon_i=-\frac{d\Psi_m}{dt} \qquad(2.1)$

Поток магнитной индукции равен:

$\Psi_m=BS{\cos \alpha =BS} \qquad (2.2)$

где $\alpha =0$ , так как нормаль к площади, которая получается при вращении стержня, параллельна направлению вектора магнитного поля (см. рис.1).

Далее будем рассматривать модуль ЭДС индукции. Подставим выражение для магнитного потока в закон (2.1), имеем:

$\left|\varepsilon_i\right|=\frac{d\left(BS\right)}{dt}=B\frac{dS}{dt} \qquad(2.3)$

В выражении (2.3) мы учли, что магнитное поле не изменяется, переменной величиной является площадь S (см. рис.1). Элементарный угол поворота стержня ( $d\varphi$ ) выразим как

$d\varphi =\omega dt\ \qquad(2.4)$

так как $\omega =const$ по условию задачи; $dt$ – время поворота стержня. Элемент площади сектора круга ( $dS$ ), который получается при движении стержня, может быть выражен как:

$dS=\frac{l^2}{2}d\varphi =\frac{l^2\omega }{2}dt\ \qquad(2.5)$

Разность потенциалов на концах нашего проводящего стержня равна по модулю ЭДС индукции:

$U=\left|\varepsilon_i\right|\ \qquad(2.6)$

Используем выражения (2.6) и формулы (2.3) и (2.5), получим:

$U=B\frac{l^2\omega}{2}\ \to \omega =\frac{2U}{Bl^2}$

Ответ

$\omega =\frac{2U}{Bl^2}$

Понравился сайт? Расскажи друзьям!