ЭДС индукции в движущихся проводниках

ЭДС – это аббревиатура трех слов: электродвижущая сила. ЭДС индукции ( $\varepsilon_i$ ) появляется в проводящем теле, которое находится в переменном магнитном поле. Если проводящим телом является, например, замкнутый контур, то в нем течет электрический ток, который называют током индукции.

Закон Фарадея для электромагнитной индукции

Основным законом, который используют при расчетах, связанных с электромагнитной индукцией является закон Фарадея. Он говорит о том, что электродвижущая сила электромагнитной индукции в контуре равна по величине и противоположна по знаку скорости изменения магнитного потока ( $\Phi_m$ ) сквозь поверхность, которую ограничивает рассматриваемый контур:

$\varepsilon_i=-\frac{d\Phi_m}{dt} \qquad (1)$

Закон Фарадея (1) записан для системы СИ. Надо учитывать, что из конца вектора нормали к контуру обход контура должен проходить против часовой стрелки. Если изменение потока происходит равномерно, то ЭДС индукции находят как:

$\varepsilon_i=-\frac{\Delta \Phi_m}{\Delta t} \qquad (2)$

Магнитный поток, который охватывает проводящий контур, может изменяться в связи с разными причинами. Это может быть и изменяющееся во времени магнитное поле и деформация самого контура, и перемещение контура в поле. Полная производная от магнитного потока по времени учитывает действие всех причин.

ЭДС индукции в движущемся проводнике

Допустим, что проводящий контур перемещается в постоянном магнитном поле. ЭДС индукции возникает во всех частях контура, которые пересекают силовые линии магнитного поля. При этом, результирующая ЭДС, появляющаяся в контуре будет равна алгебраической сумме ЭДС каждого участка. Возникновение ЭДС в рассматриваемом случае объясняют тем, что на любой свободный заряд, который движется вместе с проводником в магнитном поле, будет действовать сила Лоренца. При воздействии сил Лоренца заряды движутся и образуют в замкнутом проводнике ток индукции.

Рассмотри случай, когда в однородном магнитном поле находится прямоугольная проводящая рамка (рис.1). Одна сторона рамки может двигаться. Длина этой стороны равна l. Это и будет наш движущийся проводник. Определим, как можно вычислить ЭДС индукции, в нашем проводнике, если он перемещается со скоростью v. Величина индукции магнитного поля равна B. Плоскость рамки перпендикулярна вектору магнитной индукции. Выполняется условие $\overline{v}\bot \overline{B}$ .

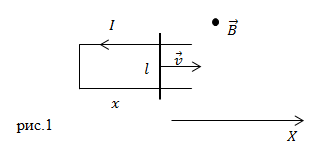
ЭДС индукции в движущихся проводниках, рисунок 1

ЭДС индукции в рассматриваемом нами контуре будет равна ЭДС, которая возникает только в подвижной его части. В стационарных частях контура в постоянном магнитном поле индукции нет.

Для нахождения ЭДС индукции в рамке воспользуемся основным законом (1). Но для начала определимся с магнитным потоком. По определению поток магнитной индукции равен:

$\Phi_m=BS\cos\ \alpha =BS \qquad (3)$

где $\cos\ \alpha =1$ , так как по условию плоскость рамки перпендикулярна направлению вектора индукции поля, следовательно, нормаль к рамке и вектор индукции параллельны. Площадь, которую ограничивает рамка, выразим следующим образом:

$S=l\cdot x \qquad (4)$

где $x=x(t)$ – расстояние, на которое перемещается движущийся проводник. Подставим выражение (2), с учетом (3) в закон Фарадея, получим:

$\varepsilon_i=-\frac{d\left(Bl\cdot x\right)}{dt}=-Bl\frac{dx}{dt}=-Blv \qquad (5)$

где v – скорость движения подвижной стороны рамки по оси X.

Если угол между направлением вектора магнитной индукции ( $\overline{B}$ ) и вектором скорости движения проводника ( $\overline{v}$ ) составляет угол $\alpha$ , то модуль ЭДС в проводнике можно вычислить при помощи формулы:

$\left|\varepsilon_i\right|=vBl{\sin \alpha} \qquad (6)$

Примеры решения задач

ПРИМЕР 1

Задание

Получите выражение для определения модуля ЭДС индукции в проводнике, длиной l, который движется в однородном магнитном поле, используя выражение для силы Лоренца. Проводник на рис.2 движется с постоянной скоростью 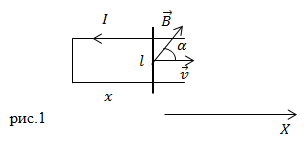$\overline{v}$ , параллельно самому себе. Вектор $\overline{B}$ перпендикулярен проводнику и составляет угол $\alpha$ с направлением $\overline{v}$ .

ЭДС индукции в движущихся проводниках, пример 1

Решение

Рассмотрим силу, с которой магнитное поле действует на заряженную частицу, движущуюся со скоростью $\overline{v}$ , мы получим:

$F_L=qvB\sin\ \alpha \qquad (1.1)$

Работа силы Лоренца на пути l составит:

$A=F_Ll=qvBl\ \sin\ \alpha \qquad (1.2)$

ЭДС индукции можно определить как работу по перемещению единичного положительного заряда:

$\varepsilon_i=\frac{A}{q}=vBl\ \sin\ \alpha \qquad (1.3)$

Ответ

$\varepsilon_i=vBl\ \sin\ \alpha$

ПРИМЕР 2

Задание

Изменение магнитного потока через контур проводника, имеющего сопротивление $R=3\cdot {10}^{-2}$ Ом за время равное $\Delta t=2$ с, составило величину $\Delta \Phi=1,2\cdot {10}^{-2}$ Вб. Какова сила тока при этом в проводнике, если изменение магнитного потока можно считать равномерным?