Электромагнитная индукция формулы

ОПРЕДЕЛЕНИЕ

Явление возникновения в переменном магнитном поле электродвижущей силы (ЭДС) называется явлением электромагнитной индукции.

Если проводник замкнут, то есть является контуром, то в нем появляется ток индукции. Явление было открыто в 1831 г. М. Фарадеем.

Основной закон электромагнитной индукции

Основной формулой, при помощи которой определяют ЭДС индукции ( $\varepsilon_i$ ), является закон Фарадея – Максвелла, больше известный как основной закон электромагнитной индукции (или закон Фарадея). В соответствии с данным законом, электродвижущая сила индукции в контуре, находящемся в переменном магнитном поле, равна по модулю и противоположна по знаку скорости изменения магнитного потока ( $\Psi_m$ ) через поверхность, которую ограничивает рассматриваемый контур:

$\varepsilon_i=-\frac{d\Psi_m}{dt} \qquad(1)$

где $\frac{d\Psi_m}{dt}$ – скорость изменения магнитного потока. Полная производная присутствующая в формуле (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) отвечает правилу Ленца. В виде (1) формула ЭДС записана для международной системы единиц (СИ), в других системах вид закона может отличаться.

При равномерном изменении магнитного потока основной закон электромагнитной индукции записывают как:

$\varepsilon_i=-\frac{\Delta \Psi_m}{\Delta t} \qquad(2)$

Формулы ЭДС индукции для частных случаев

ЭДС индукции для контура имеющего N витков, находящегося в переменном магнитном поле можно найти как:

$\varepsilon_i=-\frac{d\sum^N_{i=1}{\Psi_{mi}}}{dt}=-\frac{d\Psi}{dt} \qquad(3)$

где $\Psi=N\Psi_m$ – потокосцепление.

Если прямолинейный проводник движется в однородном магнитном поле, то в нем появляется ЭДС индукции, равная:

$\varepsilon_i=-vBl\ \qquad(4)$

где v – скорость движения проводника; l – длина проводника; B – модуль вектора магнитной индукции поля; $\overline{B}\bot \overline{v}$ .

Разность потенциалов (U) на концах прямого проводника, движущегося в однородном магнитном поле с постоянной скоростью будет равна:

$U=Blv{\sin \alpha } \qquad (5)$

где $\alpha$ – угол между направлениями векторов $\overline{v}$ и $\overline{B}$ .

При вращении плоского контура с постоянной скоростью в однородном магнитном поле вокруг оси, которая лежит в плоскости контура в нем появляется ЭДС индукции, которую можно вычислить как:

$\varepsilon_i=B_0S\omega {\sin \left(\omega t\right)-\frac{d\Psi_{m0}}{dt}} \ \qquad(6)$

где S – площадь, которую ограничивает виток; $\Psi_{m0}$ – поток самоиндукции витка; $\omega$ — угловая скорость; ( $\omega t$ ) – угол поворота контура. Необходимо заметить, что формула (5) применима, в случае, если ось вращения составляет прямой угол с направлением вектора внешнего магнитного поля ${\overline{B}}_0$ .

Если вращающаяся рамка обладает N витками, при этом самоиндукцией рассматриваемой системы можно пренебречь, то:

$\varepsilon_i=B_0S\omega {\sin \left(\omega t\right)} \ \qquad(7)$

Если проводник неподвижен в переменном магнитном поле, то ЭДС индукции можно найти как:

$\varepsilon_i=-\frac{\partial \Psi_m}{\partial t} \qquad(8)$

Примеры решения задач по теме «Электромагнитная индукция»

ПРИМЕР 1

Задание

Каково среднее значение электродвижущей силы индукции ( $\left\langle \varepsilon_i\right\rangle$ ), которая возникает в проводящем контуре, если магнитный поток, пронизывающий контур изменяется от $\Psi_{m1}=4\cdot {10}^{-2}$ Вб до $\Psi_{m2}=0$ Вб за время равное $\Delta t=2\cdot {10}^{-3}$ c?

Решение

В качестве основы для решения задачи используем основной закон электромагнитной индукции в виде:

$\left\langle \varepsilon_i\right\rangle =\left|\frac{\Delta \Psi_m}{\Delta t}\right|=\frac{\Psi_1-\Psi_2}{\Delta t}\ \qquad(1.1)$

Проведем вычисления:

$\left\langle \varepsilon_i\right\rangle =\frac{4\cdot{10}^{-2}}{2\cdot{10}^{-3}}=20\ (B)$

Ответ

$\left\langle \varepsilon_i\right\rangle$ =20 В

ПРИМЕР 2

Задание

В однородное магнитное поле помещена прямоугольная рамка, одна сторона которой может двигаться (рис.1). Длина подвижной части равна l. Масса подвижной перемычки равна m. Перемычка без трения скользит вниз с постоянной скоростью v. Величина индукции магнитного поля B. Направление вектора 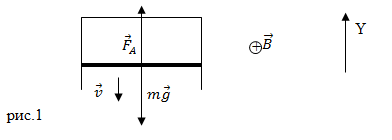$\overline{B}$ перпендикулярно плоскости контура. Каково сопротивление подвижной части контура? Самоиндукцию и сопротивление остальной части контура можно не учитывать.

Решение

При движении проводника в магнитном поле в нем возникает ЭДС индукции, а так как, в общем, мы имеем замкнутый контур, то в проводнике течет ток индукции. На проводник с током в магнитном поле действует сила Ампера. Для того чтобы движущаяся часть проводника двигалась с постоянной скоростью сила Ампера должна компенсировать силу тяжести, которая действует на перемычку. По второму закону Ньютона:

$m\overline{g}+{\overline{F}}_A=0\ \qquad(2.1)$

Сила тяжести направлена вниз, следовательно, сила Ампера будет направлена вверх (рис.1). В проекции на ось Y выражения (2.1) имеем:

$mg=F_{A} \qquad(2.2)$

Модуль силы Ампера найдем как:

$F_{A} =IBl{\sin \alpha =IBl} \qquad (2.3)$

где ${\sin \alpha } =1$ , так как $\overline{B}$ перпендикулярен направлению течения тока. Используя выражения (2.2) и (2.3) выразим силу тока, текущую через проводник:

$IBl=mg\ \to I=\frac{mg}{Bl}\ \qquad(2.4)$

Сопротивление проводника можно найти используя закон Ома:

$R=\frac{U}{I}=\frac{\varepsilon_i}{I} \qquad(2.5)$

Модуль ЭДС индукции найдем, используя основной закон индукции и используя тот факт, что при равномерном движении площадь рассматриваемого контура за время $\Delta t$ изменяется как $\Delta S=lv\Delta t$ :