Теорема Кирхгофа

Основная идея Гюйгенса-Френеля в теории интерференции и дифракции волн света заключается в том, что световое возмущение в некоторой точке, появляется как следствие наложения (суперпозиции) вторичных волн, которые испускаются поверхностью, расположенной между рассматриваемой точкой и источником света. Кирхгоф создал математическую форму записи принципа Гюйгенса-Френеля. Он показал, что вышеназванный принцип можно считать некоторой формой интегральной теоремы. Теория дифракции Кирхгофа применяется к дифракции скалярных волн. Скалярная теория может быть использована для исследования проблем инструментальной оптики.

Интегральная терема Кирхгофа

Интегральная теорема Кирхгофа дает возможность выразить амплитуду светового поля в точке наблюдения через интеграл по любой поверхности, которая охватывает точку наблюдения.

В теореме Кирхгофа решение однородного волнового уравнения в произвольной точке поля представлено через величину искомого параметра, его первую производную во всех точках произвольной замкнутой поверхности, которая окружает рассматриваемую точку.

Пусть волна будет монохроматической и скалярной:

$U\left(x,y,z,t\right)=U_0\left(x,y,z\right)e^{-i\omega t} \qquad (1)$

$U_0\left(x,y,z\right)$ – комплексная амплитуда светового поля. В вакууме часть этой волны, зависящая от координат, удовлетворяет волновому уравнению Гельмгольца:

$\left({\nabla}^2+k^2\right)U_0=0 \qquad (2)$

где $k=\frac{\omega}{c}$ , так как само поле света удовлетворяет волновому уравнению.

Пусть V – объем, ограниченный произвольной замкнутой поверхностью S, точка А некоторая точка внутри рассматриваемого объема. Тогда одной из форм интегральной теоремы Кирхгофа – Гельмгольца:

$U_0(A)=\frac{1}{4\pi}\oint_S{\left[U_0\frac{\partial}{\partial n}\left(\frac{e^{iks}}{s}\right)-\frac{e^{iks}}{s} \frac{\partial U_0}{\partial n}\right]dS} \qquad (3)$

где $\frac{\partial}{\partial n}$ – означает дифференцирование вдоль внутренней нормали к поверхности S. s – расстояние от точки А до точки с координатами ( $x,y,z$ ).

Примеры решения задач

ПРИМЕР 1

Задание

Покажите на основе теоремы Кирхгофа, что поле световой волны в точке наблюдения можно представить как сумму полей вторичных источников волн.

Решение

Допустим, что источник света один (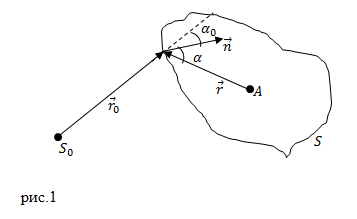 $S_0$ ) и является точечным и сферически симметричным. Точкой наблюдения станет точка А, ее будет охватывать замкнутая поверхность S, причем такая, что источник света находится снаружи (рис.1).

Рассмотрим рис.1. Здесь $\overline{r}$ – радиус-вектор из точки А в точку поверхности S. ${\overline{r}}_0$ – радиус-вектор из источника световых волн в точку на поверхности S. $\overline{n}$ – внутренняя нормаль к поверхности S. Угол $\alpha$ – угол между нормалью $\overline{n}$ и вектором $\overline{r}.\ {\alpha}_0$ – угол между нормалью и вектором ${\overline{r}}_0$ . Запишем теорему Кирхгофа для точки А:

$U_0(A)=\frac{1}{4\pi}\oint_S{\left[U_0({\overline{r}}_0)\frac{\partial}{\partial n}\left(\frac{e^{ikr}}{r}\right)-\frac{e^{ikr}}{r} \frac{\partial U_0({\overline{r}}_0)}{\partial n}\right]dS} \qquad (1.1)$

Поле точечного источника, обладающего сферичной симметрией можно записать как:

$E_0\left({\overline{r}}_0\right)=A_0\frac{e^{ikr_0}}{r_0} \qquad (1.2)$

Подставим правую часть выражения (1.2) в теорему Кирхгофа (1.1), имеем:

$U_0(A)=\frac{A_0}{4\pi}\oint_S{\left[\frac{e^{ikr_0}}{r_0}\frac{\partial}{\partial n}\left(\frac{e^{ikr}}{r}\right)-\frac{e^{ikr}}{r} \frac{\partial}{\partial n}\left(\frac{e^{ikr_0}}{r_0}\right)\right]dS} \qquad (1.3)$

Функция $\frac{e^{ikr}}{r}$ зависит только от r. Производную от нее по любому направлению можно выразить, как производную по r, умноженную на косинус угла между вектором $\overline{r}$ и направлением дифференцирования. В нашей задаче направлением дифференцирования будет направление внутренней нормали $\overline{n},$ а именно:

${\cos (\widehat{\overline{n,}\overline{r}})}=-{\cos \alpha} \qquad (1.4)$

В таком случае, имеем:

$\frac{\partial}{\partial n}\left(\frac{e^{ikr}}{r}\right)=\frac{d}{dr}\left(\frac{e^{ikr}}{r}\right)\left(-{\cos \alpha}\right)=\left[ik\frac{e^{ikr}}{r}-\frac{1}{r^2}e^{ikr}\left(-{\cos \alpha}\right)\right] \qquad (1.5)$

Так как длина волны света существенно меньше, чем любое рассматриваемое нами расстояние, то:

$\frac{1}{r}\ll k=\frac{2\pi}{\lambda}\to \frac{1}{r^2}\ll \frac{k}{r} \qquad (1.6)$

В виду (1.6) формулу (1.5) преобразуем как:

$\frac{\partial}{\partial n}\left(\frac{e^{ikr}}{r}\right)\approx -ik\frac{e^{ikr}}{r}{\cos \alpha} \qquad (1.7)$

По аналогии получаем:

$\frac{\partial}{\partial n}\left(\frac{e^{ikr_0}}{r_0}\right)\approx ik\frac{e^{ikr_0}}{r_0}{\cos {\alpha}_0} \qquad (1.8)$

Подставим правые части выражений (1.7) и (1.8) в (1.3), имеем:

$U_0(A)=-\frac{A_0}{4\pi}\oint_S{\left[\frac{e^{ikr_0}}{r_0}(ik\frac{e^{ikr}}{r}{\cos \alpha )}+\frac{e^{ikr}}{r}\left.(ik\frac{e^{ikr_0}}{r_0}{\cos {\alpha}_0})\right]dS} \qquad (1.9)$

Будем считать, что любое световое поле можно представить как систему излучений точечных источников $U_{0}\left(\overline{r}\right)=A_0\frac{e^{ikr_0}}{r_0}$ . Тогда выражение (1.9) запишем как:

$U_0(A)=-\frac{A_0ik}{4\pi}\oint_S{\left[U_{0}\left(\overline{r}\right)(\frac{e^{ikr}}{r}{\cos \alpha )}+\frac{e^{ikr}}{r}\left.\left(U_{0}\left(\overline{r}\right){\cos {\alpha}_0}\right)\right]dS} \qquad (1.10)$

Слагаемые в подынтегральном выражении отличаются только косинусами, примем во внимание, что:

$\frac{k}{4\pi}=\frac{1}{2\lambda}\qquad \left(1.11\right)$

получим:

$U_0(A)=-\frac{A_0i}{2\lambda}\oint_S{\left[U_{0}\left(\overline{r}\right)\frac{e^{ikr}}{r}({\cos \alpha +{\cos {\alpha}_0}}\left.)\right]dS} \qquad (1.12)$

Выражение (1.12) показывает, что поле в точке наблюдения валяется суммой полей вторичных источников, которые находятся на замкнутой поверхности S.

ПРИМЕР 2

Задание

Дайте анализ амплитуды излучения вторичных источников света, в точке наблюдения используя результаты примера 1.

Решение

Амплитуда пропорциональна: площади поверхности излучения, если взять элементарную площадку, то поверхности $dS$ ; комплексной амплитуде поля $E_{0}\left(\overline{r}\right)$ в точке расположения вторичного источника. Амплитуда обратно пропорциональна расстоянию (r) от вторичного источника до точки наблюдения. Амплитуда в точке наблюдения обладает фазовым множителем $e^{ikr}$ . Этот множитель определяется запаздыванием фазы ( $kr$ ) в точке наблюдения по отношению к фазе вторичного источника. Помимо этого амплитуда вторичного источника пропорциональна выражению $- \frac{i}{2\lambda}({\cos \alpha +{\cos {\alpha}_0}})$ . Данное выражение называют коэффициентом наклона. Он описывает связь излучательной способности вторичного источника с направлением волны, которая приходит к нему и от направления волны уходящей от вторичного источника.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Теорема Кирхгофа

Интегральная терема Кирхгофа

Примеры решения задач