Дифракция Фраунгофера на щели

Определение и общие сведения о дифракции Фраунгофера на щели

ОПРЕДЕЛЕНИЕ

Дифракцией Фраунгофера (дифракцией в параллельных лучах) называют дифракцию плоских волн.

Этот вид задач рассматривает дифракцию лучей, в которых источник света и точка наблюдения находятся на бесконечно большом удалении от препятствия, на котором происходит дифракция. Для того чтобы на практике реализовать данный вид дифракции источник света размещают в фокусе собирающей линзы, при этом картину дифракции наблюдают в фокальной плоскости другой собирающей линзы, расположенной сзади препятствия. Картина дифракции является «дифракционным изображением источника света». Данный вид дифракции описывают аналитически.

Теорема Бабине

Если при дифракции препятствиями служат экраны, то два экрана называют дополнительными, если отверстия в одном из них совпадают по форме, размерам и расположению, непрозрачным участкам на втором экране.

При дифракции Фраунгофера на экране интенсивность света после дифракции в любом направлении, которое не совпадает с направлением распространения первичной волны, попадающей на экран, должна быть такой же, как при дифракции на дополнительном экране.

Дифракция на узкой длинной щели

Пусть монохроматический свет падает на узкую длинную щель нормально ее плоскости. Амплитуда волны (A) в побочном фокусе линзы равна (точке наблюдения):

$A\left(\varphi \right)=A_0\frac{{\sin \left\{\frac{kb{\sin \varphi}}{2}\right\}}}{\frac{kb{\sin \varphi}}{2}} \qquad (1)$

где $\varphi$ – угол дифракции, который отсчитывают от внешней нормали к фронту падающей волны; $A_0$ – амплитуда волны в центре картины дифракции (при $\varphi =0$ ); b – ширина щели; $k=\frac{2\pi}{\lambda}$ – волновое число.

Условие минимумов при дифракции на узкой щели имеет вид:

$A\left(\varphi \right)=0,\ {\sin \varphi =\pm \frac{m\lambda}{b}} \qquad (2)$

где m – целое число, принимающее значение $m=1,2,3\dots$

Условием максимумов (второе выражение является приближенным) в рассматриваемом случае являются:

$\left\{ \begin{array}{c} \varphi =0\ ,A=A_{0},\ n=0; \\ {\sin \varphi}=\pm \left(2n+1\right)\frac{\lambda}{2b},\ \left(n=1,2,3\dots \right)\qquad (3) \end{array}$

Расстояние от центра картины дифракции до первого минимума увеличивается при уменьшении ширины щели. Центральный максимум интенсивности при этом увеличивает свою ширину и уменьшает свою высоту. При $b=\lambda$ первый максимум уходит в бесконечность. Интенсивность постепенно спадает от центра к краям в плоскости наблюдения. При увеличении b картина дифракции сужается, главный максимум выделяется резче. При $b\gg \lambda$ на экране получают четкое изображение источника света (по законам геометрической оптики).

Дифракция на прямоугольном отверстии

Если рассматривают дифракцию на прямоугольном отверстии с высотой a и шириной b, то направление распространения света после дифракции задают при помощи двух углов (например, $\alpha$ и $\beta$ ). Это углы между направлением луча дифрагированного света и осью X (для $\alpha$ ) и Y (для $\beta$ ). Оси проводят параллельно сторонам отверстия.

В случае перпендикулярного падения света на плоскость отверстия минимумы интенсивности света после дифракции будут определены формулами:

$b{\sin (\frac{\pi}{2}-\alpha )}=\pm m\lambda;\ a{\sin (\frac{\pi}{2}-\beta )}=\pm n\lambda \qquad (4)$

где m, n – целые неотрицательные числа.

Дифракция на круглом отверстии

Допустим, что свет распространяется от точечного источника, и падает на круглое отверстие перпендикулярно его плоскости, то дифракционную картину составляет система светлых и темных колец. Расположение максимумов и минимумов интенсивности определяет выражение:

${\sin \varphi =\ \frac{k_m}{R}}m\lambda \qquad (5)$

где $\varphi$ – угол дифракции, который связан с фокусным расстоянием линзы (F), как ( $\varphi =\frac{r}{F},\ r$ – расстояние от центра картины дифракции до рассматриваемой точки;); R – радиус отверстия; $m=1, 2,3\dots$ — порядок максимума или минимума; величины $k_{max}$ для разных порядков максимума:

$\begin{array}{cc} m & k_{max} \\ 1 & 0 \\ 2 & 0,41 \\ 3 & 0,44 \end{array} \qquad (6)$

$k_{min}$ для разных порядков максимума:

$\begin{array}{cc} m & k_{min} \\ 1 & 0,61 \\ 2 & 0,56 \\ 3 & 0,54 \end{array} \qquad (7)$

Уменьшение радиуса отверстия приводит к расплыванию картины дифракции. При увеличении R картина дифракции стягивается в точку.

Примеры решения задач

ПРИМЕР 1

Задание

На щель шириной b падает, перпендикулярно ее плоскости, свет с длиной волны, равной $\lambda$ . Картину дифракции наблюдают на экране, который расположен параллельно щели. Каково расстояние от щели до экрана (l), если ширина центрального максимума дифракции равна a? Считайте, что $b\ll l$ .

Решение

Сделаем рисунок.

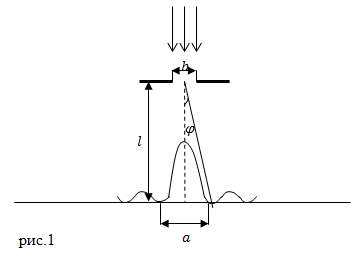
В данной задаче мы можем рассматривать происходящее как дифракцию Фраунгофера на узкой щели. Условие минимумов при дифракции на узкой щели запишем как:

$A\left(\varphi \right)=0,\ {\sin \varphi =\pm \frac{m\lambda}{b}} \qquad (1.1)$

где m=1 в нашем случае, то есть выражение (1.1) преобразуем к виду:

${\sin \varphi =\frac{\lambda}{b}} \qquad (1.2)$

Из прямоугольного треугольника (см. рис.1) имеем:

$\text{tg}\ \varphi =\frac{a}{2l}\to l=\frac{a}{2\ \text{tg}\ \varphi}=\frac{a}{2\ \text{tg}\ ({\arcsin \frac{\lambda}{b}})}$

Ответ

$l=\frac{a}{2\ \text{tg}\ ({\arcsin \frac{\lambda}{b}})}$

ПРИМЕР 2

Задание

Каково угловое положение первых минимумов, которые расположены по обе стороны от центрального максимума при дифракции Фраунгофера, если свет длины волны $\lambda$ падает на длинную щель ширины b под углом ${\alpha}_0$ к ее нормали?