Работа идеального газа

Рассмотрим газ, который находится в цилиндре, закрытом поршнем (рис.1).

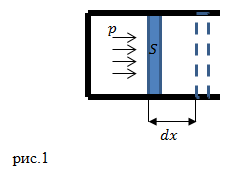
Пусть газ при расширении передвинет поршень на малое расстояние $dx$ . Таким образом, газ выполнит работу над поршнем ( $\delta A$ ):

$\delta A=Fdx=pSdx=pdV \qquad (1)$

где F – сила, с которой газ действует на поршень, S – площадь поршня; p – давление газа на поршень; $dV=Sdx$ – изменение объёма газа под поршнем. Результирующая работа газа, если его объем изменяется от $V_1$ до $V_2,$ находится как:

$A=\int^{V_2}_{V_1}{pdV} \qquad (2)$

Более конкретный результат интегрирования определяет зависимость $p(V)$ . Формула (2) для вычисления работы справедлива для изменения объема всех видов тел (газа, жидкости и твердого тела).

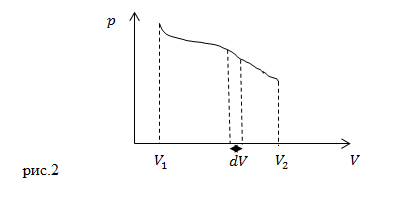
Часто работу газа изображают при помощи графиков в осях $p(V)$ (рис.2). Если объем газа увеличивается на $dV$ , то работа газа ( $\delta A=pdV$ ) – это площадь криволинейной трапеции с основанием $dV$ на рис. 2. Суммарная работа, которую совершил газ, изменяя объем от $V_1$ до $V_2$ , определена площадью, которая ограничивается осью абсцисс, кривой $p=f(V)$ и прямыми $V_1$ и $V_2$ .

Работа идеального газа для отдельных процессов

В изобарном процессе ( $p=const$ ) работа вычисляется при помощи формулы:

$A_{p=const}=p\int^{V_2}_{V_1}{dV=p\left(V_2-V_1\right)} \qquad (3)$

В изохорном процессе работа газа равна нулю, так как изменения объема не происходит:

$A_{V=const}=0 \qquad (4)$

Найдем работу для изотермического процесса ( $T=const$ ):

$A_{T=const}=\int^{V_2}_{V_1}{pdV=\int^{V_2}_{V_1}{\frac{m}{\mu}\frac{T}{V}dV=\frac{mT}{\mu}\int^{V_2}_{V_1}{\frac{dV}{V}=\frac{mT}{\mu}}{\ln \left(\frac{V_2}{V_1}\right)}.}} \qquad (5)$

где из уравнения Менделеева – Клапейрона: $p=\frac{m}{\mu}\frac{T}{V}. (\mu$ – молярная масса газа; m – масса газа). Получили, что для изотермического процесса работа равна:

$A_{T=const}=\frac{mT}{\mu}l{n \left(\frac{V_2}{V_1}\right)} \qquad (6)$

Для адиабатного процесса, который проходит без обмена теплом окружающей среды и газа работу проще найти из первого начала термодинамики:

$\Delta Q=A+\Delta U \qquad (7)$

Так как $\Delta Q=0,$ то получаем, что в адиабатном процессе газ выполняется работу за счет уменьшения внутренней энергии:

$A=-\Delta U=\frac{i}{2}\frac{m}{\mu}R\left(T_1-T_2\right) \qquad (8)$

где i – число степеней свободы молекулы газа.

Примеры решения задач

ПРИМЕР 1

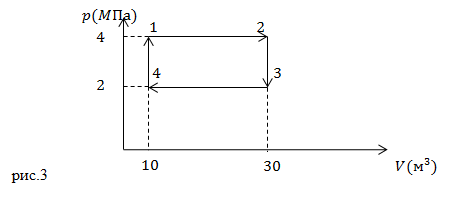
Задание

Чему равна работа, которая совершается в круговом процессе, изображенном на рис.3?

Решение

В представленном цикле 1-2-3-4 изменение объема газа происходит в процессах: 1-2 и 3-4. Процессы 2-3 и 4-2 протекают при постоянном объеме. В процессе 1-2 объем газа увеличивается, это значит, что газ совершает работу ( $A_{1-2}>0$ ). В процессе 3-4 объем газа уменьшается, следовательно, работу совершают над газом ( $A_{3-4}<0$ ). Работа в круговом процессе будет равна:

$A=A_{1-2}+A_{3-4} \qquad (1.1)$

Мы знаем, что работу можно трактовать как площади, в нашем случае, площади прямоугольников:

$A_{1-2}=S_{1} \qquad (1.2)$

где $S_{1}$ – площадь прямоугольника, вершины которого обозначены точками 1-2-30-10.

$S_{1}=\left(30-10\right)4\cdot {10}^6=8\cdot {10}^7$

$A_{3-4}=S_{2} \qquad (1.3)$

где $S_{2}$ – площадь прямоугольника, вершины которого обозначены точками 3-4-10-30.

$S_{2}=\left(30-10\right)2\cdot {10}^6=4\cdot {10}^7$

Результирующая работа равна:

$A=S_{1}-S_{2}=4\cdot {10}^7(J)$

Работу в цикле можно было найти сразу как площадь фигуры, которая определена кривой цикла, в нашем случае это площадь прямоугольника 1-2-3-4:

$A=S=\left(30-10\right)\left(4\cdot {10}^6-2\cdot {10}^6\right)=4\cdot {10}^7(J)$

Ответ

$A=4\cdot {10}^7$ Дж

ПРИМЕР 2

Задание

Какое количество теплоты подводят к идеальному двухатомному газу ( $i=5$ ) в изотермическом процессе, если работа его расширения составила A=2 кДж? Какое количество тепла потребуется при изобарном расширении?

Решение

1) Для изотермического процесса первое начало термодинамики:

$\Delta Q=A+\Delta U\ (2.1)$

преобразуется к виду:

$\Delta Q_{T=const}=A \qquad (2.2)$

так как при T=const внутренняя энергия идеального газа не изменяется. В изотермическом процессе к газу подводят 2 кДж теплоты.

2) Для изобарного расширения. Чтобы найти количество теплоты, подводимое системе, снова воспользуемся первым началом термодинамики (2.1). Работа нам известна, нужно найти изменение внутренней энергии газа. Мы знаем, что в изобарном процессе:

$A=p\Delta V \qquad (2.3)$