Формула работы идеального газа
Работа в термодинамике
Работа в термодинамике вычисляется как:
![Rendered by QuickLaTeX.com \[A=\int^{V_2}_{V_1}{pdV} \qquad (1)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-83209968ffebc53b0ffb303bd9351120_l3.png)
где ![]() – начальный объем системы;
– начальный объем системы; ![]() – конечный объем. Работа считается большей нуля, если работу выполняет система (газ) над внешними силами.
– конечный объем. Работа считается большей нуля, если работу выполняет система (газ) над внешними силами.
Работу можно вычислить исходя из первого начала термодинамики:
![]()
где ![]() – количество теплоты, которое система получает;
– количество теплоты, которое система получает; ![]() – изменение внутренней энергии системы. Если в качестве термодинамической системы выступает идеальный газ, то выражение (2) можно записать как:
– изменение внутренней энергии системы. Если в качестве термодинамической системы выступает идеальный газ, то выражение (2) можно записать как:
![]()
где i – число степеней свободы молекулы идеального газа; ![]() – количество вещества; m – масса газа;
– количество вещества; m – масса газа; ![]() – молярная масса газа; R – универсальная газовая постоянная;
– молярная масса газа; R – универсальная газовая постоянная; ![]() – изменение температуры газа в рассматриваемом процессе. Выражения (1),(2) и (3) записаны в интегральном виде.
– изменение температуры газа в рассматриваемом процессе. Выражения (1),(2) и (3) записаны в интегральном виде.
Элементарная работа идеального газа (![]() ) равна:
) равна:
![]()
Или из первого начала термодинамики в дифференциальном виде следует, что:
![]()
Работа идеального газа в частных случаях
При изохорном процессе (![]() ) работа газа равна нулю.
) работа газа равна нулю.
В изобарном процессе (![]() ) работу вычисляют как:
) работу вычисляют как:
![]()
где ![]() – конечный и начальный объемы газа; p – давление газа.
– конечный и начальный объемы газа; p – давление газа.
При изотермическом процессе (![]() ) работу газа можно найти как:
) работу газа можно найти как:
![]()
При адиабатном процессе работу газ совершает за счет уменьшения своей внутренней энергии, и она равна:
![]()
или
![Rendered by QuickLaTeX.com \[A=\frac{\nu RT_1}{\gamma -1}\ \left(1-{\left(\frac{V_1}{V_2}\right)}^{\gamma -1}\right) \qquad(8)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-055770d4c84af456f59d6c4acff6486c_l3.png)
где ![]() – показатель адиабаты.
– показатель адиабаты.
Примеры решения задач по теме «Работа идеального газа»
| Задание | Идеальный газ занимал объем равный |
| Решение | В качестве основы для решения задачи используем формулу для вычисления работы в этом процессе где Из (1.2) выразим конечный объем газа( Подставим полученное выражение для объема (1.3) в выражение для работы (1.1): Проведем вычисления работы газа: |
| Ответ | |
| Задание | На рис. 1 изображен круговой процесс, проводимый в идеальном газе. Фигура, изображенная на рисунке, является эллипсом. Какую работу совершает газ за один цикл? Используйте данные приведенные на рисунке.
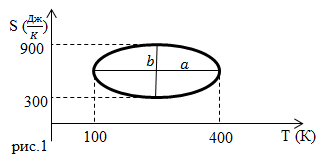
|
| Решение | Для обратимого процесса, который в идеальном газе возможен, элементарное изменение энтропии Следовательно, количество теплоты, получаемое идеальным газом можно найти как: Исходя из геометрического смысла интеграла, количество теплоты, полученное системой в одном цикле ( где Из первого начала термодинамики, теплота, подводимая к газу, расходуется на совершение им работы и изменение внутренней энергии: Однако, из рисунка 1 видно, что цикл замкнутый, а внутренняя энергия является функцией состояния, следовательно, за полный цикл ее изменение равно нулю Значит, работа газа за один цикл равна: Проведем вычисления: |
| Ответ |











