Формула идеального газа

ОПРЕДЕЛЕНИЕ

Для того чтобы формулы и законы в физике были более простыми для понимания и использования применяют разного рода модели и упрощения. Такой моделью является идеальный газ. Модель в науке – это упрощенная копия реальной системы.

Модель отражает наиболее существенные характеристики и свойства процессов и явлений. В модели идеального газа учитываются только основные свойства молекул, которые требуются для того, чтобы объяснить основы поведения газа. Идеальный газ напоминает реальный газ в довольно узком интервале давлений (p) и температур (T).

Самым важным упрощением идеального газа является то, что кинетическая энергия молекул считается гораздо большей, чем потенциальная энергия их взаимодействия. Столкновения молекул газа описывают при помощи законов упругого соударения шаров. Движение молекул считают прямолинейными в промежутках между столкновениями. Эти допущения позволяют получить специальные уравнения, которые называют уравнениям состояния идеального газа. Данные уравнения можно применять к описанию состояний реального газа при невысоких температурах и давлениях. Уравнения состояния и можно назвать формулами для идеального газа. Приведем также другие основные формулы, которые используют при исследовании поведения и свойств идеального газа.

Уравнения состояния идеального

Уравнение Менделеева — Клапейрона

$pV=\frac{m}{\mu }RT\qquad \qquad(1)$

где p – давление газа; V – объем газа; T — температура газа по шкале Кельвина; m – масса газа; $\mu$ – молярная масса газа; $R=8,31\ \frac{J}{mol\cdot K}$ — универсальная газовая постоянная.

Уравнением состояния идеального газа так же является выражение:

$p=nkT \qquad(2)$

где n – концентрация молекул газа в рассматриваемом объеме; $k=1,38\cdot {10}^{-23}\frac{J}{K}$ .

Основное уравнение молекулярно-кинетической теории

При помощи такой модели, как идеальный газ, получают основное уравнение молекулярно-кинетической теории (МКТ) (3). Которое говорит о том, что давление газа -это результат огромного числа ударов его молекул о стенки сосуда, в котором газ находится.

$p=\frac{2}{3}n\left\langle E\right\rangle =\frac{1}{3}nm_0{\left\langle v_{kv}\right\rangle }^2 \qquad(3)$

где $\left\langle E\right\rangle$ — средняя кинетическая энергия поступательного движения молекул газа; $n=\frac{N}{V}$ — концентрация молекул газа (N – число молекул газа в сосуде; V – объем сосуда); $m_0$ – масса молекулы газа; $\left\langle v_{kv}\right\rangle$ – среднеквадратичная скорость молекулы.

Внутренняя энергия идеального газа

Так как в идеальном газе принимают потенциальную энергию взаимодействия молекул равной нулю, то внутренняя энергия равна сумме кинетических энергий молекул:

$U=\frac{i}{2}\frac{m}{\mu }kTN_A=\frac{i}{2}\frac{m}{\mu }RT=\frac{i}{2}\nu RT\ \qquad(4)$

где i – число степеней свободы молекулы идеального газа; $N_A=6,02\cdot {10}^{-23}\frac{1}{mol}$ – число Авогадро; $\nu$ – количество вещества. Внутренняя энергия идеального газа определена его термодинамической температурой (T) и пропорциональна массе.

Работа идеального газа

Для идеального газа в изобарном процессе ( $p=const$ ) работу вычисляют при помощи формулы:

$A_{p=const}=p\int^{V_2}_{V_1}{dV=p\left(V_2-V_1\right)} \qquad (5)$

В изохорном процессе работа газа равна нулю, так как изменения объема нет:

$A_{V=const}=0\ \qquad(6)$

Для изотермического процесса ( $T=const$ ):

$A_{T=const}=\frac{mT}{\mu }{ln \left(\frac{V_2}{V_1}\right)} \qquad(7)$

Для адиабатного процесса ( $\Delta Q=0$ ) работа равна:

$A=-\Delta U=\frac{i}{2}\frac{m}{\mu }R\left(T_1-T_2\right) \qquad(8)$

где i – число степеней свободы молекулы газа.

Примеры решения задач по теме «Идеальный газ»

ПРИМЕР 1

Задание

Какова плотность смеси идеальных газов при температуре T и давлении p, если масса одного газа $m_1,$ его молярная масса ${\mu }_1$ , масса второго газа $m_2,$ молярная масса ${\mu }_2$ ?

Решение

По определению плотность однородного вещества ( $\rho$ ) это:

$\rho =\frac{m}{V} \qquad(1.1)$

где m – масса всего вещества; V – его объем. Масса смеси газов находится как сумма отдельных компонент смеси:

$m=m_1+m_2 \qquad(1.2)$

Осталось найти объем, который занимает смесь газов при заданных условиях. Для этого запишем уравнение Менделеева – Клапейрона для смеси:

$pV=\nu RT\ \qquad(1.3)$

где количество вещества смеси ( $\nu$ ) найдем как:

$\nu ={\nu }_1+{\nu }_2=\frac{m_1}{{\mu }_1}+\frac{m_2}{{\mu }_2}\ \qquad(1.4)$

Выразим объем смеси, учитывая (1.4):

$V=\left(\frac{m_1}{{\mu }_1}+\frac{m_2}{{\mu }_2}\ \right)\frac{RT}{p} \qquad(1.5)$

Подставим формулы (1.2) и (1.5) в (1.1), получим:

$\rho =\frac{\left(m_1+m_2\right)p}{\left(\frac{m_1}{{\mu }_1}+\frac{m_2}{{\mu }_2}\ \right)RT}$

Ответ

$\rho =\frac{\left(m_1+m_2\right)p}{\left(\frac{m_1}{{\mu }_1}+\frac{m_2}{{\mu }_2}\ \right)RT}$

ПРИМЕР 2

Задание

Выберите из перечисленных ниже процессов, какому процессу в идеальном газе соответствует график, изображенный на рис.1? Изохорному, изобарному, адиабатному.

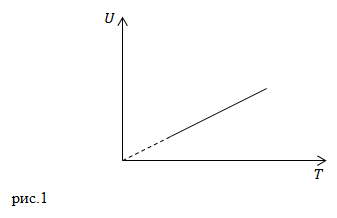
Решение

Внутренняя энергия идеального газа определяется как:

$U=\frac{i}{2}\frac{m}{\mu }RT \qquad(2.1)$

Она для любого процесса пропорциональная температуре. При постоянной массе одного и того же газа в изохорном, адиабатном и изобарном процессах мы получим график, изображенный на рис.1

Понравился сайт? Расскажи друзьям!

Советуем прочитать: