Модуль упругой деформации

Определение и модуль упругой деформации

ОПРЕДЕЛЕНИЕ

Деформацией называют внешнее механическое воздействие на тело, которое приводит к изменению его объема и (или) формы.

Деформация в твердом теле называется упругой, если она пропадает после того, как нагрузку с тела сняли.

ОПРЕДЕЛЕНИЕ

Модулем упругой деформации (модулем упругости) называют некоторую совокупность параметров, которые характеризуют способность твердого тела претерпевать деформацию при воздействии на него.

В общем случае модуль упругости (E) определяют как

$E=\frac{d\sigma}{d\varepsilon} \qquad (1)$

где $\sigma$ – напряжение; $\varepsilon$ – относительная деформация. Надо помнить, что данное определение справедливо для линейного отрезка диаграммы напряжений, то есть когда деформацию можно считать упругой. На данном участке диаграммы величина E определена тангенсом угла наклона прямолинейного участка диаграммы.

В зависимости от типа деформации, направления действия деформирующей силы различают несколько модулей упругости. Наиболее часто используемые:

модуль Юнга;
модуль сдвига;
модуль объемной упругости;
коэффициент Пуассона и др.

Модуль Юнга

Модуль Юнга используют при характеристике деформация растяжения (сжатия) упругого тела, при этом деформирующая сила действует по оси тела. Модуль Юнга чаще всего определяют используя закон Гука:

$E=\frac{\sigma}{\varepsilon} \qquad (2)$

Модуль Юнга, равен напряжению, появляющемуся в стержне, если его относительное удлинение равно единице (или $E=\sigma$ при двойном удлинении длины тела). На практике кроме резины при упругой деформации двойного удлинения невозможно достичь, тело рвется.

Коэффициент упругости и модуль Юнга связаны как:

$k=\frac{SE}{l_0} \qquad (3)$

где $l_0$ – длина тела до деформации; S – площадь поперечного сечения.

Единицей измерения модуля Юнга служит паскаль.

Модуль сдвига

При помощи модуля сдвига (G) характеризуют способность тела оказывать сопротивление изменению формы тела (при этом объем сохраняется). Находят модуль сдвига как:

$G=\frac{Fh}{S\triangle s} \qquad (4)$

$\triangle s$ – абсолютный сдвиг слоев параллельных по отношению друг к другу; h — расстояние между слоями; F – сила, вызывающая сдвиг, параллельная сдвигающимся слоям тела.

Если вещество является однородным и изотропным, то модуль сдвига связан с модулем Юнга выражением:

$G=\frac{E}{2\left(1+\nu \right)} \qquad (5)$

где $\nu$ – коэффициент Пуассона для материала, который зависит от природы вещества. Иногда обозначается буквой $\mu$ .

Модуль объемной упругости

Модуль объемной упругости (модуль объемного сжатия) (K) – отражает способность тела к изменению объема при действии объемного напряжения, которое одинаково по всем направлениям. Его определяют выражением:

$K=-V\frac{dp}{dV} \qquad (6)$

где V – объем тела; p – давление, оказываемое на тело.

Если тело является изотропным, то:

$K=\frac{E}{3\left(1-2\nu \right)} \qquad (7)$

Примеры решения задач

ПРИМЕР 1

Задание

Стержень из металла закреплен неподвижно за один конец так, что он висит вертикально. К нижнему концу стержня прикреплен груз массой m. Первоначальная длина стержня была равна l, площадь поперечного сечения S. Длина стержня после того как к нему подвесили груз увеличилась на 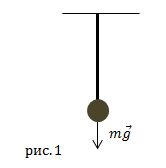$\triangle l$ . Чему равен модуль Юнга (E) материала из которого сделан стержень? Массой стержня можно пренебречь в сравнении с массой груза.

Решение

Сила (F), растягивающая стержень равна по модулю силе тяжести, которая действует на груз, который закреплен на конце стержня:

$F=mg \qquad (1.1)$

Абсолютное удлинение растянутого тела связано с модулем упругости выражением:

$E=\frac{\sigma}{\varepsilon} \qquad (1.2)$

где:

$\varepsilon =\frac{\triangle l}{l};\ \sigma=\frac{F}{S}$

То есть формула (1.2) преобразуется к виду:

$E=\frac{Fl}{\triangle l\ S}=\frac{mg\ l}{\triangle l\ S}$

Ответ

$E=\frac{mg\ l}{\triangle l\ S}$

ПРИМЕР 2

Задание

Проволока длинной l и диаметром d закреплена за концы горизонтально. К середине этой проволоки подвесили груз массы m. Проволока растянулась, и точка подвеса опустилась на h. Каков модуль Юнга материала проволоки?

Решение

Сделаем рисунок.

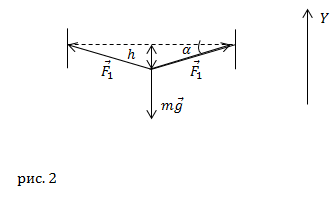
В равновесии мы имеем (см. рис.1):

${\overrightarrow{F}}_1+{\overrightarrow{F}}_1+m\overrightarrow{g}=0 \qquad (2.1)$

где ${\overrightarrow{F}}_1$ – сила натяжения проволоки. В проекции на ось Y:

$2F_1{\sin \alpha =mg} \qquad (2.2)$

Так как угол $\alpha$ мал, то можно считать:

${\sin \alpha \approx \alpha \approx \text{tg}\ \alpha =\frac{h}{\frac{l}{2}}}=\frac{2h}{l} \qquad (2.3)$

Используя выражения (2.2) и (2.3) запишем:

$F_1=\frac{mgl}{4h} \qquad (2.4)$

Модуль Юнга для нашего случая равен:

$E=\frac{F_1l}{\triangle l\ S} \qquad (2.5)$

где удлинение проволоки найдем как:

$\triangle l=\frac{l}{{\cos \alpha}}-l=l\left(\frac{1-{\cos \alpha}}{{\cos \alpha}}\right)\approx l\frac{{\alpha}^2}{2}=\frac{l}{2}\frac{4h^2}{l^2}=\frac{2h^2}{l} \qquad (2.6)$

Подставим в (2.5) формулы (2.4) и (2.6), имеем:

$E=\frac{mgl}{4h}\frac{l}{\frac{2h^2}{l}\ S}=\frac{4mgl^3}{8\pi d^2h^3}=\frac{mgl^3}{2\pi d^2h^3}$