Электродинамика для чайников
Электродинамика для чайников
Часто электромагнитное поле делят на электрическое и магнитное поле. Свойства электромагнитных полей, принципы их взаимодействия изучает особый раздел физики, который называют электродинамикой. В самой электродинамике выделяют следующие разделы:
- электростатику;
- магнитостатику;
- электродинамику сплошной среды;
- релятивистскую электродинамику.
Электродинамика является основой для изучения и развития оптики (как раздела науки), физики радиоволн. Этот раздел науки является фундаментом для радиотехники и электротехники.
Классическая электродинамика в описании свойств электромагнитных полей и принципов их взаимодействия использует систему уравнений Максвелла (в интегральной или дифференциальной формах), дополняя ее системой материальных уравнений, граничными и начальными условиями. Согласно Максвеллу имеется два механизма возникновения магнитного поля. Это наличие токов проводимости (перемещающийся электрический заряд) и переменное во времени электрическое поле (наличие токов смещения).
Уравнения Максвелла
Основные законы классической электродинамики (система уравнений Максвелла) является результатом обобщения экспериментальных данных и стали квинтэссенцией электродинамики неподвижной среды. Уравнения Максвелла делят на структурные и материальные. Структурные уравнения записывают в двух видах: в интегральном и дифференциальном виде. Запишем уравнения Максвелла в дифференциальном виде (система СИ):
![]()
где ![]() – вектор напряженности электрического поля;
– вектор напряженности электрического поля; ![]() – вектор магнитной индукции.
– вектор магнитной индукции.
![]()
где ![]() — вектор напряженности магнитного поля;
— вектор напряженности магнитного поля;![]() – вектор диэлектрического смещения;
– вектор диэлектрического смещения; ![]() – вектор плотности тока.
– вектор плотности тока.
![]()
где ![]() – плотность распределения электрического заряда.
– плотность распределения электрического заряда.
![]()
Структурные уравнения Максвелла в дифференциальной форме характеризуют электромагнитное поле в каждой точке пространства. Если заряды и токи распределены в пространстве непрерывно, то интегральная и дифференциальная формы уравнений Максвелла эквивалентны. Однако, если имеются поверхности разрыва, то интегральная форма записи уравнений Максвелла является более общей. (Интегральную форму записи уравнений Максвелла можно посмотреть в разделе «Электродинамика»). Для достижения математической эквивалентности интегральной и дифференциальной форм уравнений Максвелла дифференциальную запись дополняют граничными условиями.
Из уравнений Максвелла следует, что переменное магнитное поле порождает переменное электрическое поле и наоборот, то есть эти поля неразрывны и образуют единое электромагнитное поле. Источниками электрического поля могут быть либо электрические заряды, либо переменное во времени магнитное поле. Магнитные поля возбуждаются движущимися электрическими зарядами (токами) или переменными электрическими полями. Уравнения Максвелла не являются симметричными относительно электрического и магнитного полей. Это происходит из-за того, что электрические заряды существуют, а магнитных нет.
Материальные уравнения
Систему структурных уравнений Максвелла дополняют материальными уравнениями, которые отражают связь векторов ![]() c параметрами, характеризующими электрические и магнитные свойства вещества.
c параметрами, характеризующими электрические и магнитные свойства вещества.
![]()
![]()
![]()
где ![]() – относительная диэлектрическая проницаемость,
– относительная диэлектрическая проницаемость, ![]() – относительная магнитная проницаемость,
– относительная магнитная проницаемость, ![]() — удельная электропроводность,
— удельная электропроводность, ![]() – электрическая постоянная,
– электрическая постоянная, ![]() – магнитная постоянная. Среда в таком случае считается изотропной, неферромагнитной, несегнетоэлектрической.
– магнитная постоянная. Среда в таком случае считается изотропной, неферромагнитной, несегнетоэлектрической.
Примеры решения задач
| Задание | Запишите систему структурных уравнений Максвелла для стационарных полей. |
| Решение | Если речь идет о стационарных полях, то имеется в виду, что: Источниками электрического поля в этом случае являются только электрические заряды. Источники магнитного поля при этом токи проводимости. В нашем случае электрическое и магнитное поля являются независимыми друг о друга. Это дает возможность исследовать отдельно постоянное электрическое и отдельно магнитное поле. |
| Задание | Запишите функцию плотности тока смещения в зависимости от расстояния от оси соленоида ( |
| Решение | В качестве основ для решения задачи используем уравнение из системы уравнений Максвелла в интегральном виде:
Определим ток смещения как: Найдем частную производную Из формул (2.1) и (2.3) для Используем материальное равнение: считая вещество изотропным, тогда: Используем формулу (2.2) и выражение (2.6) получим: При Изобразим график изменения модуля 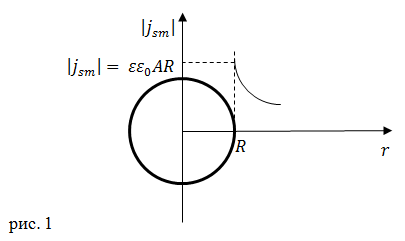
|
| Ответ | При |






![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{c} rot\ \overline{E}=0 \qquad \left(1.1\right); \\ rot\ \overline{H}=\overline{j} \qquad \left(1.2\right); \\ div\ \overline{D}=\rho \qquad \left(1.3\right); \\ div\ \overline{B}=0 \qquad \left(1.4\right). \end{array} \right\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-3033482aa711d4c583810c54a286ba78_l3.png)





