Центробежный момент инерции

Центробежный момент инерции тела

Допустим, что имеется система координат с началом в точке O и осями OX; OY; OZ. По отношению к данным осям центробежными моментами инерции (произведениями инерции) называются величины $J_{xy},\ J_{yz},\ J_{zx}$ , которые определяются равенствами:

$J_{xy}=\sum{\Delta m_ix_iy_i};\ J_{yz}=\sum{\Delta m_iy_iz_i};\ J_{zx}=\sum{\Delta m_iz_ix_i} \qquad (1)$

где $\Delta m_i$ – массы материальных точек, на которые разбивают тело; $x_i,\ y_i,\ z_i$ – координаты соответствующих материальных точек.

Центробежный момент инерции обладает свойством симметрии, это следует из его определения:

$J_{xy}=J_{yx}\ \qquad (2)$

Если тело можно считать сплошным (непрерывным), то определение центробежного момента инерции записывают как:

$J_{xy}=\int_V{\rho xy\ dV; }J_{yz}=\int_V{\rho yz\ dV; }J_{zx}=\int_V{\rho zx\ dV\ } \qquad (3)$

Центробежные моменты тела могут быть положительными и отрицательными, при определённом выборе осей OXYZ они могут обращаться в ноль.

Для центробежных моментов инерции существует аналог теоремы Штейнберга. Если рассмотреть две системы координат: $CXYZ$ и $OX'Y'Z'$ . Одна из этих систем имеет начало координат в центе масс тела (точка C), оси систем координат являются попарно параллельными ( $CX||\ OX'; CY||\ OY'; \ CZ||\ OZ'$ ). Пусть в системе координат $OX'Y'Z'$ координатами центра масс тела являются ( $a,b,c$ ), тогда:

$\left\{ \begin{array}{c} J_{x'y'}=J_{xy}+mab; \\ J_{y'z'}=J_{yz}+mbc; \\ J_{x'z'}=J_{xz}+mac, \end{array} \qquad (4) \right$

где $m$ – масса тела.

Главные оси инерции тела

Пусть однородное тело имеет ось симметрии. Построим координатные оси так, чтобы ось OZ была направлена вдоль оси симметрии тела. Тогда, как следствие симметрии каждой точке тела с массой $\Delta m_i$ и координатами $x_i{,y}_i, z_i$ соответствует точка, имеющая другой индекс, но такую же массу и координаты: ${-x}_i{,-y}_i,z_i$ . В результате получаем, что:

$\sum{\Delta m_ix_iz_i=0}; \sum{\Delta m_iy_iz_i=0} \qquad \(4)$

так как в данных суммах все слагаемые имеют свою равную по величине, но противоположную по знаку пару. Выражения (4) эквивалентны записи:

$J_{xz}=0; \ J_{yz}=0\ \qquad (5)$

Мы получили, что осевая симметрия распределения масс по отношению к оси OZ характеризуется равенством нулю двух центробежных моментов инерции (5), которые содержат среди своих индексов наименование этой оси. В таком случае ось OZ называется главной осью инерции тела для точки О.

Главная ось инерции не всегда является осью симметрии тела. Если тело обладает плоскостью симметрии, то любая ось, которая перпендикулярна этой плоскости, является главной осью инерции для точки O, в которой ось пересекает рассматриваемую плоскость. Равенства (5) отображают условия того, что ось OZ является главной осью инерции тела для точки O (начала координат). Если выполняются условия:

$J_{xy}=0; \ J_{yz}=0\ \qquad (6)$

то ось OY будет для точки O главной осью инерции.

В том случае, если выполняются равенства:

$J_{xy}=0; \ J_{yz}=0\ ; \ J_{zx}=0 \qquad (7)$

то все три координатные оси системы координат OXYZ являются главными осями инерции тела для начала координат.

Моменты инерции тела по отношению к главным осям инерции называются главными моментами инерции тела. Главные оси инерции, которые построены для центра масс тела, носят название главных центральных осей инерции тела.

Если тело обладает осью симметрии, то она является одной из главных центральных осей инерции тела, поскольку центр масс находится на этой оси. В том случае, если тело имеет плоскость симметрии, то ось, нормальная к этой плоскости и проходящая через центр масс тела является одной из главных центральных осей инерции тела.

Понятие главных осей инерции в динамике твердого тела имеет существенное значение. Если вдоль них направить оси координат OXYZ, то все центробежные моменты инерции становятся равными нулю, при этом значительно упрощаются формулы, которые следует применять при решении задач динамики. С понятием о главных осях инерции связано решение задач о динамическом уравнении тела находящегося во вращении и о центре удара.

Момент инерции тела ( и центробежный в том числе) в международной системем единиц измеряются в:

$\left[J\right]=kg\cdot m^2$

Центробежный момент инерции сечения

Центробежным моментом инерции сечения (плоской фигуры) относительно двух взаимно нормальных осей (OX и OY) называют величину, равную:

$J_{xy}=\int_S{xy\ dS} \qquad (8)$

выражение (8) говорит о том, что центробежный момент инерции сечения относительно взаимно перпендикулярных осей есть сумма произведений элементарных площадок ( $dS$ ) на расстояния от них до рассматриваемых осей, по всей площади S.

Единицей измерения моментов инерции сечения в СИ является:

$\left[J\right]=m^4$

Центробежный момент инерции сложного сечения по отношению к любым двум взаимно нормальным осям равен сумме центробежных моментов инерции составляющих его частей относительно этих осей.

Примеры решения задач

ПРИМЕР 1

Задание

Получите выражение для центробежного момента инерции прямоугольного сечения относительно осей (X,Y).

Решение

Сделаем рисунок.

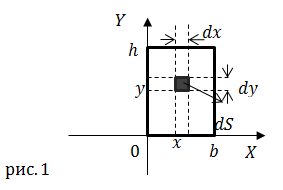
Для определения центробежного момента инерции $J_{xy}$ выделим из имеющегося прямоугольника элемент его площади (рис.1) $dS$ , площадь которой равна:

$dS=dxdy\ \qquad (1.1)$

На первом этапе решения задачи найдем центробежный момент инерции ( $dJ_{xy}$ ) вертикальной полосы, имеющей высоту $h$ и ширину $dx$ , которая находится на расстоянии $x$ от оси Y (учтем, что при интегрировании для всех площадок в избранной вертикальной полоске величина $xdx$ является постоянной):

$dJ_{xy}=\int^h_0{xydS=}\int^h_0{xydxdy=xdx\int^h_0{ydy=}}xdx\frac{h^2}{2} \qquad (1.2)$

На втором этапе решения задачи $dJ_{xy}$ проинтегрируем, двигаясь по горизонтали, учитывая, что $0\le x\le b$ :

$J_{xy}=\int^b_0{xdx\frac{h^2}{2}}=\frac{h^2}{2}\frac{b^2}{2}$

Ответ

$J_{xy}=\frac{h^2b^2}{4}$

ПРИМЕР 2

Задание	Чему равен центробежный момент инерции прямоугольной плоской однородно й пластины, относительно осей X Y прямоугольной декартовой системы координат, которые проходят через ее центр масс рис.2?
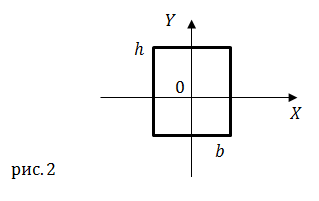
Ответ	Центробежный момент инерции прямоугольника относительно осей X и Y (рис.2) равен нулю, так как эти оси совпадают с его осями симметрии.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Центробежный момент инерции

Центробежный момент инерции тела

Главные оси инерции тела

Центробежный момент инерции сечения

Примеры решения задач