Момент инерции прямоугольного сечения

Определение и общие понятия о моменте инерции

Осевым (экваториальным) моментом инерции сечения по отношению к некоторой оси называют взятую по всей его площади S сумму произведений элементарных площадок $dS$ на квадраты их расстояний от этой оси:

$J_y=\int_S{x^2dS\ ;}J_x=\int_S{y^2dS} \qquad (1)$

Полярным моментом инерции сечения относительно точки (полюса) называют сумму произведений элементарных площадок $dS$ на квадраты расстоянии от них до полюса, при этом сумма берется по всей площади S:

$J_p=\int_S{{\rho}^2dS} \qquad (2)$

где ${\rho}^2=x^2+y^2$ (рис.1)

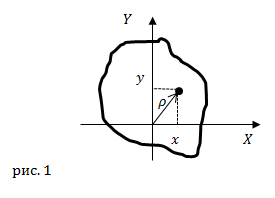
Момент инерции прямоугольного сечения, рисунок 1

Если оси, по отношению к которым известны моменты инерции взаимно перпендикулярны, то легко найти полярный момент инерции относительно точки пересечения этих осей, как сумму осевых моментов инерции.

Центробежным моментом инерции сечения по отношению к некоторым взаимно перпендикулярным осям называют сумму произведений элементарных площадок $dS$ на их расстояния от этих осей, взятых по всей площади сечения S:

$J_{xy}=\int_S{xy\ dS} \qquad (3)$

Осевой момент инерции прямоугольного сечения

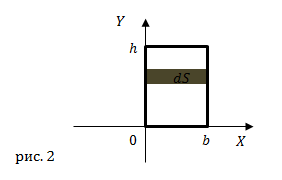
Найдем осевой момент инерции прямоугольника, который имеет высоту h и ширину $b$ относительно оси X, которая проходит через основание прямоугольника (рис.2).

Выделим из нашего прямоугольника элементарную площадку dS (рис.2). Основания этой площадки параллельны осям X и Y. Высота полоски составляет dy, ширина b. Площадь данной полоски равна:

$dS=bdy \qquad (4)$

Расстояние от полоски до оси X равно y. Используя второе выражение из (1), для момента инерции сечения относительно оси X имеем:

$J_x=\int_S{y^2dS=\int^h_0{y^2}bdy=b\frac{h^3}{3}} \qquad (5)$

Для получения момента инерции прямоугольного сечения относительно оси Y элементарную полоску выделяют параллельно оси Y. Проводят аналогичную последовательность действий, при этом получают:

$J_y=h\frac{b^3}{3} \qquad (6)$

Центробежный момент инерции прямоугольного сечения

Центробежный момент инерции прямоугольного сечения относительно осей XY(рис. 2) ( $J_{xy}$ ) равен:

$J_{xy}=\frac{b^2h^2}{4} \qquad (7)$

Если оси X и Y провести через центр тяжести прямоугольного сечения, то центробежный момент инерции равен нулю, так ка эти оси совпадают с осями симметрии.

Примеры решения задач

ПРИМЕР 1

Задание

Получите выражение для осевого момента инерции для прямоугольной пластинки ширины b высотой h, если она вращается относительно оси Y рис.3.

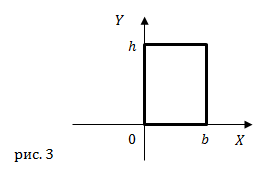
Момент инерции прямоугольного сечения, пример 1

Решение

Для получения осевого момента инерции для прямоугольного сечения 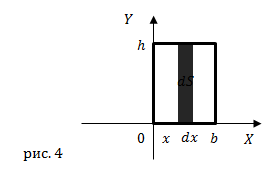$J_y$ выделим на нашем прямоугольнике малую прямоугольную площадь ( $dS$ ), стороны которой параллельны сторонам прямоугольника (рис. 4). При этом ширина $dS$ равна $dx$ , расстояние от выделенного элемента до оси Y равно x.

Момент инерции прямоугольного сечения, пример 2

В качестве основы для нахождения момента инерции сечения воспользуемся формулой:

$J_y=\int_S{x^2dS} \qquad (1.1)$

Площадь выделенного элементарного прямоугольника найдем как:

$dS=hdx \qquad (1.2)$

Подставим $dS$ в выражение (1.1), учтём в пределах интегрирования, что $0\le x\le b$ :

$J_y=\int^b_0{x^2hdx=h\frac{b^3}{3}\ .}$

Ответ

$J_y=h\frac{b^3}{3}$ .

ПРИМЕР 2

Задание

Каковы осевые моменты инерции прямоугольного сечения относительно осей X и Y, проходящих через центр тяжести параллельно сторонам прямоугольника ( $J_x,J_y$ )?

Решение

Сделаем рисунок.

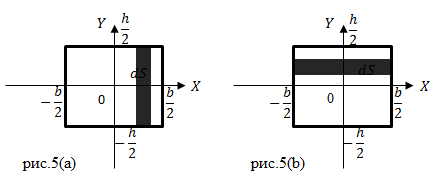
Найдем осевой момент инерции прямоугольного сечения относительно оси Y. Для этого выделим элементарный прямоугольных площадью $dS$ на расстоянии x от оси Y ширина которого равна $dx$ . Воспользуемся формулой:

$J_y=\int_S{x^2dS} \qquad (2.1)$

где:

$dS=hdx \qquad (2.2)$

Учтем выражение (2.2) проинтегрируем (2.1) при $- \frac{b}{2}\le x\le \frac{b}{2}$ :

$J_y=\int^{\frac{b}{2}}_{-\frac{b}{2}}{x^2hdx=h{\left.\frac{x^3}{3}\right|}^{\frac{b}{2}}_{-\frac{b}{2}}=2h\frac{b^3}{3\cdot 8}=h\frac{b^3}{12}} \qquad (2.3)$

Найдем осевой момент инерции прямоугольного сечения относительно оси X. Для этого выделим элементарный прямоугольных площадью $dS$ на расстоянии y от оси X ширина которого равна $dy$ . Воспользуемся формулой: