Осевой момент инерции

Определение и общие понятия осевого момента инерции

ОПРЕДЕЛЕНИЕ

Осевым (или экваториальным) моментом инерции сечения относительно оси называется величина, которую определяют как:

$J_x=\int_S{y^2dS\ ; \ J_y=\int_S{x^2dS}} \qquad (1)$

Выражение (1) обозначает, для вычисления осевого момента инерции берется по всей площади S сумма произведений бесконечно малых площадок ( $dS$ ) умноженных на квадраты расстояний от них до оси вращения:

Сумма осевых моментов инерции сечения относительно взаимно перпендикулярных осей (например, относительно осей X и Y в декартовой системе координат) дают полярный момент инерции ( $J_p$ ) относительно точки пересечения этих осей:

$J_x+J_y=J_p \qquad (2)$

ОПРЕДЕЛЕНИЕ

Полярным моментом инерции называют момент инерции сечением по отношению к некоторой точке.

Осевые моменты инерции всегда больше нуля, так как в их определениях (1) под знаком интеграла стоят величина площади элементарной площадки ( $dS$ ), всегда положительная и квадрат расстояния от этой площадки до оси.

Если мы имеем дело с сечением сложной формы, то часто при расчетах используют то, что осевой момент инерции сложного сечения по отношению к оси равен сумме осевых моментов инерции частей этого сечения относительно той же оси. Однако следует помнить, что нельзя суммировать моменты инерции, которые найдены относительно разных осей и точек.

Осевой момент инерции относительно оси проходящей через центр тяжести сечения имеет наименьшее значение из всех моментов относительно параллельных с ней осей. Момент инерции относительно любой оси ( $J$ ) при условии ее параллельности с осью, проходящей через центр тяжести равен:

$J=J_0+a^2S\ \qquad (3)$

где $J_0$ – момент инерции сечения относительно оси проходящей через центр тяжести сечения; $S$ – площадь сечения; $a$ – расстояние между осями.

Примеры решения задач

ПРИМЕР 1

Задание

Чему равен осевой момент инерции равнобедренного треугольного сечения относительно оси Z, проходящей через центр тяжести (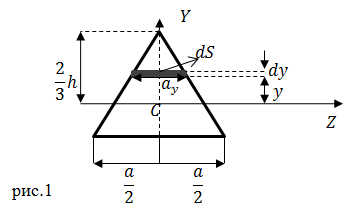 $C$ ) треугольника, параллельно его основанию? Высота треугольника равна $h$ .

Решение

Выделим на треугольном сечении прямоугольную элементарную площадку $dS$ (см. рис.1). Она находится на расстоянии $y$ от оси вращения, длина одной ее стороны $a_y$ , другая сторона $dy$ . Из рис.1 следует, что:

$a_y=a\frac{\frac{2h}{3}-y}{h} \qquad (1.1)$

Площадь выделенного прямоугольника с учетом (1.1) равна:

$dS=a_ydy=a\frac{\frac{2h}{3}-y}{h}dy \qquad (1.2)$

Для нахождения осевого момента инерции используем его определение в виде:

$J_Z=\int_S{y^2dS}=\int^{\frac{2h}{3}}_{-\frac{h}{3}}{y^2}a\frac{\frac{2h}{3}-y}{h}dy=\frac{a}{3h}\int^{\frac{2h}{3}}_{-\frac{h}{3}}{y^2}\left(2h-3y\right)dy=\frac{a}{3h}\left\{2h{\left.\frac{y^3}{3}\right|}^{\frac{2h}{3}}_{-\frac{h}{3}}-3{\left.\frac{y^4}{4}\right|}^{\frac{2h}{3}}_{-\frac{h}{3}}\right\}=\frac{ah^3}{36}$

Ответ

$J_Z=\frac{ah^3}{36}$

ПРИМЕР 2

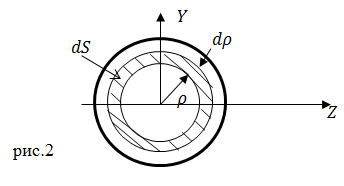
Задание

Найдите осевые моменты инерции относительно перпендикулярных осей X и Y (рис.2) сечения в виде круга диаметр которого равен d.

Решение

Для решения задачи удобнее начать с нахождения полярного момента относительно центра сечения ( $J_p$ ). Все сечение разобьем на бесконечно тонкие кольца толщиной $d\rho$ , радиус которых обозначим $\rho$ . Тогда элементарную площадь найдем как:

$dS=2\pi \rho d\rho \ \qquad (2.1)$