Формула заряда конденсатора, q

ОПРЕДЕЛЕНИЕ

Назначение конденсатора состоит в накоплении электрического заряда и возможности отдавать его в цепи. Способность конденсатора накапливать электрический заряд зависит от основной характеристики конденсатора – электрической емкости.

По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.

Формула заряда конденсатора

Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:

$q=CU\ \qquad(1)$

где q – величина заряда одной из обкладок конденсатора, а $U={\varphi }_1-{\varphi }_2$ – разность потенциалов между его обкладками.

Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.

Заряд на пластинах плоского конденсатора равен:

$q=\frac{\varepsilon {\varepsilon }_0S}{d}U \qquad(3)$

где ${\varepsilon }_0$ – электрическая постоянная; ${S}$ – площадь каждой (или наименьшей) пластины; ${d}$ – расстояние между пластинами; $\varepsilon$ – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.

Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:

$q=\frac{2\pi \varepsilon {\varepsilon }_0l}{ln\left(\frac{R_2}{R_1}\right)}U \qquad(4)$

где l – высота цилиндров; $R_2$ – радиус внешней обкладки; $R_1$ – радиус внутренней обкладки.

Заряд на обкладках сферического конденсатора найдем как:

$q=\frac{4\pi \varepsilon {\varepsilon }_0R_1R_2}{R_2-R_1}U \qquad(5)$

где $R_1{;\ R}_2$ – радиусы обкладок конденсатора.

Заряд конденсатора связан с энергией поля (W) внутри него:

$W=\frac{qU}{2}=\frac{q^2}{2C} \qquad(6)$

Из формулы (6) следует, что заряд можно выразить как:

$q=\frac{2W}{U}=\sqrt{2CW} \qquad(7)$

Рассмотрим последовательное соединение из N конденсаторов ( рис. 1).

$q_1=q_2=\dots =q_N \qquad(8)$

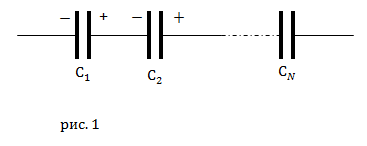
Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.

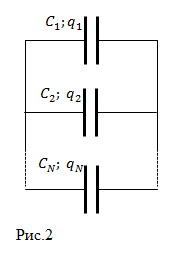
При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.

$q=q_1+q_2+\dots +q_N \qquad(9)$

Примеры решения задач по теме «Заряд конденсатора»

ПРИМЕР 1

Задание

Каковы заряды на обкладках конденсаторов, если они имеют емкости 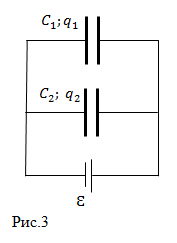$C_1=3\cdot {10}^{-6}$ Ф и $C_2=6\cdot {10}^{-6}$ Ф, соединены последовательно и присоединены к батарее с ЭДС равной $\varepsilon=120$ В (рис.3)? Чему равен суммарный заряд соединения?

Решение

Разности потенциалов на обкладках конденсаторов будут при таком соединении равны:

$U_1=U_2=\varepsilon\ \qquad(1.1)$

Заряд на первом конденсаторе при этом равен:

$q_1=C_1\varepsilon\ \qquad(1.2)$

Заряд на обкладках второго конденсатора:

$q_2=C_2\varepsilon\ \qquad(1.3)$

Суммарный заряд системы можно найти как:

$q=q_1+q_2 \qquad(1.4)$

Проведем вычисления:

$q_1=3\cdot {10}^{-6}\cdot 120=3,6\cdot {10}^{-4}\ \left(Kl\right)$

$q_2=6\cdot {10}^{-6}\cdot 120=7,2\cdot {10}^{-4}\ \left(Kl\right)$

Тогда суммарный заряд равен:

$q=3,6\cdot {10}^{-4}+7,2\cdot {10}^{-4}=10,8\cdot {10}^{-4}\ \left(Kl\right)$

Ответ

$q_1=3,6\cdot {10}^{-4}$ Кл; $q_2=7,2\cdot {10}^{-4}$ Кл; $q=10,8\cdot {10}^{-4}$ Кл

ПРИМЕР 2

Задание

Емкость пускового устройства электрического двигателя равна C. Энергии имеющейся в конденсаторе достаточно для того чтобы поднять груз массы m на высоту h. Чему равен заряд конденсатора?

Решение

При поднятии груза на высоту h происходит переход энергии поля конденсатора ( $W_c$ ) в потенциальную энергию тела ( $E_p$ ), поднятого над Землей, поэтому запишем:

$W_c=E_p\ \qquad(2.1)$