Примеры индукции

Пример нахождения формулы для расчета вектора магнитной индукции с применением закона Био-Савара-Лапласа

Сначала напомним, что закон Био-Савара-Лапласа в совокупности с принципом суперпозиции, используют для нахождения вектора магнитной индукции $\overline{B}$ в любой точке поля. Пусть магнитное поле создается в вакууме элементом проводника с током, который можно считать прямолинейным. Для элементарного магнитного поля ( $d\overline{B}$ ) закон Био-Савара-Лапласа имеет вид:

$d\overline{B}=\frac{{\mu}_0}{4\pi}\frac{I}{r^3}\left[d\overline{l}\overline{r}\right] \qquad (1)$

где I – сила тока; $d\overline{l}$ – вектор элемента проводника, равный по модулю длине проводника, совпадающий по направлению с направлением течения тока; $\overline{r}$ – радиус-вектор, который проводят от элементарного проводника к точке, в которой ищут поле; ${\mu}_0=4\pi \cdot {10}^{-7}\frac{Gn}{m}$ – магнитная постоянная. Вектор $d\overline{B}$ перпендикулярен плоскости, в которой лежат $d\overline{l}$ и $\overline{r}$ , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта). Силовыми линиями элементарного проводника с током являются окружности, центры которых лежат на проводнике. Для того чтобы получить суммарное поле, которое создает проводник с током используют принцип суперпозиции, который для непрерывного проводника записывается как:

$\overline{B}=\int_l{d\overline{B}\ \left(2\right).}$

В однородном и изотропном магнетике при равных условиях магнитное поле в вакууме ( ${\overline{B}}_0$ ) связано с магнитным полем в веществе ( $\overline{B}$ ) как:

$\overline{B}=\mu {\overline{B}}_0 \qquad (3)$

где $\mu$ – магнитная проницаемость вещества.

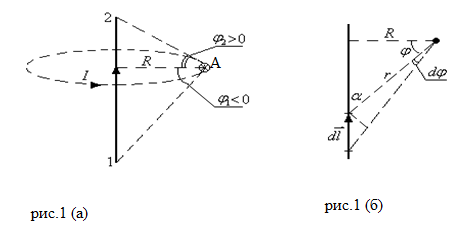
Найдем вектор индукции магнитного поля, которое создано прямым тонким проводом, по которому течет ток I (рис.1(a)) для точки, находящейся на расстоянии R от провода в вакууме. При этом концам участка соответствуют углы ${\varphi}_1$ и ${\varphi}_2$ .

Силовыми линиями магнитного поля при этом являются окружности, плоскости которых перпендикулярны проводнику, а центры лежат на проводнике. В точке А вектор магнитной индукции направлен перпендикулярно плоскости рис.1 и от нас. В точке А модуль магнитного поля элемента проводника dl, в соответствии с законом Био- Савара – Лапласа запишем как:

$d\overline{B}=\frac{{\mu}_0}{4\pi}\frac{Idl{\sin \alpha}}{r^2} \qquad (4)$

Принимая во внимание, что ${\sin \alpha} ={\cos \varphi}$ и $dl{\cos \varphi} =rd\varphi ;\ R=r{\cos \varphi}$ (см. рис.1 (б)), преобразуем формулу (4).

$d\overline{B}=\frac{{\mu}_0I}{4\pi R}{\cos \varphi \ d\varphi} \qquad (5)$

Применяя принцип суперпозиции, получим:

$B=\int^{{\varphi}_2}_{{\varphi}_1}{\frac{{\mu}_0I}{4\pi R}{\cos \varphi \ d\varphi} =}\frac{{\mu}_0I}{4\pi R}\left({\sin {\varphi}_2} -{\sin {\varphi}_1} \right)=\frac{{\mu}_0I}{4\pi R}({\cos \left({\alpha}_1\right)-{\cos ({\alpha}_2)}} )$

Пример использования теоремы о циркуляции для нахождения индукции магнитного поля

Напомним теорему о циркуляции в вакууме: В магнитном поле циркуляция вектора магнитной индукции вдоль замкнутого контура L равна сумме токов (с учетом их знаков), которые охватывает контур L:

$\oint_L{\overline{B}d\overline{r}={\mu}_0\sum^N_{m=1}{I_m}} \qquad(6)$

ток в выражении (6) имеет знак плюс, если он связан правилом правого винта с направлением обхода контура.

Рассмотрим соленоид бесконечно длинный. Соленоидом называют проводник, намотанный на цилиндр. Пусть ток, текущий по нему равен I, число витков соленоида N, длина соленоида l. Найдем поле внутри соленоида без сердечника ( $\mu =1$ ). Для данного соленоида магнитное поле можно считать однородным. Силовые линии поля при этом имеют направление параллельное оси соленоида. Направление силы тока и $\overline{B}$ связывает правило правого винта.

В качестве кривой, по которой будем рассматривать циркуляцию, используем прямоугольник (рис.2).

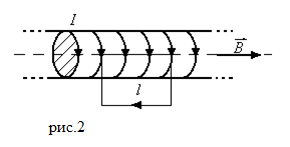
По теореме о циркуляции для избранного контура имеем:

$\oint_L{\overline{B}d\overline{r}=Bl={\mu}_0NI\ \to B={\mu}_0\frac{N}{l}}I$

Примеры решения задач

ПРИМЕР 1

Задание

Используя формулу для расчета магнитного поля, которое создает прямой проводник с током: $B=\frac{{\mu}_0I}{4\pi R}\left({\sin {\varphi}_2} -{\sin {\varphi}_1} \right)$ , получите формулу для поля, которое создает проводник бесконечной длины.

Решение

Сделаем рисунок.

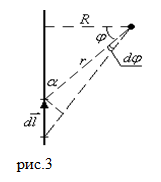
Для бесконечного проводника см. рис. 3 в расчетной формуле следует считать ${\varphi}_1=-\frac{\pi}{2}$ , а ${\varphi}_2=\frac{\pi}{2}$ . Подставим в выражение:

$B=\frac{{\mu}_0I}{4\pi R}\left({\sin {\varphi}_2} -{\sin {\varphi}_1} \right)=\frac{{\mu}_0I}{4\pi R}\left({\sin \left(\frac{\pi}{2}\right)} -{\sin \left(-\frac{\pi}{2}\right)} \right)=\frac{{\mu}_0I}{2\pi R}$

Ответ

$B=\frac{{\mu}_0I}{2\pi R}$

ПРИМЕР 2

Задание

Какой будет индукция магнитного поля в центре проводящей рамки в виде квадрата со стороной $a$ , если сила тока в рамке равна I?

Решение

Сделаем рисунок.

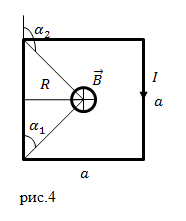
Из соображений симметрии можно заключить, что суммарное поле в центре рамки можно найти как:

$B=4B_1 \qquad (2.1)$

где $B_1$ – магнитное поле, которое создает одна сторона рамки в центре квадрата, которую найдем как:

$B_1=\frac{{\mu}_0I}{4\pi R}\left({\cos \left({\alpha}_1\right)-{\cos \left({\alpha}_2\right)}} \right) \qquad (2.2)$

Расстояние R (см. рис.4) равно половине стороны квадрата:

$R=\frac{a}{2} \qquad (2.3)$

Кроме того из рисунка 4 следует, что:

${\alpha}_2=180-\alpha_1 \qquad (2.4)$

$\alpha_1=45^\circ ;\ \ \alpha_2=180-45^\circ =135^\circ$

Преобразуем формулу (2.2), используя (2.3) и (2.4), получаем:

$B_1=\frac{{\mu}_0I}{2\pi a}\left({\cos \left(45^\circ \right)-{\cos \left(135^\circ \right)}} \right)=\frac{{\mu}_0I}{2\pi a}\left(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\right)=\frac{{\mu}_0I}{\sqrt{2}\pi a} \qquad (2.5)$

Окончательно получаем:

$B=4\frac{{\mu}_0I}{\sqrt{2}\pi a}=2\sqrt{2}\frac{{\mu}_0I}{\pi a}$

Ответ

$B=2\sqrt{2}\frac{{\mu}_0I}{\pi a}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Примеры индукции

Пример нахождения формулы для расчета вектора магнитной индукции с применением закона Био-Савара-Лапласа

Пример использования теоремы о циркуляции для нахождения индукции магнитного поля

Примеры решения задач