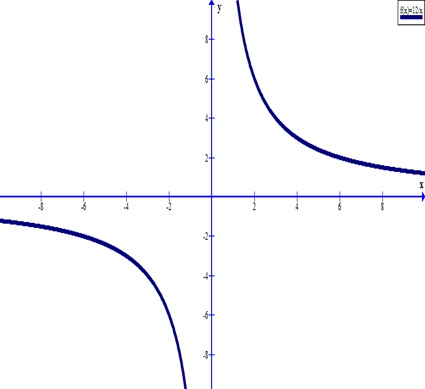
Постройте график функции y=12/x

DWQA Questions › Постройте график функции y=12/x

0 +1 -1

Asya Админ. спросил 6 лет назад

Здравствуйте!
В задании сказано:
«Постройте график функции y = 12 / x».
Помогите, пожалуйста, выполнить. Очень нужно подробное объяснение!
Спасибо!

1 ответ

0 +1 -1

Asix Админ. ответил 6 лет назад

Задание.
Постройте график функции y = 12 / x.

Решение.
Подобные функции с дробями обычно имеют графики в виде гиперболы. Проанализируем функцию.
Дробь, которая описывает функцию, в своем числителе имеет постоянное число 12, а вот знаменатель функции будет менять свое значение, т.к. в нем стоит переменная х.
В случаях, когда в знаменателе дроби стоит переменная, необходимо определить, для каких значений функция может существовать, а для каких нет. В этом нам поможет математическое правило, согласно которому нельзя делить на ноль. Поэтому для заданной функции существует единственное ограничение:

$x\ne 0$

Других ограничений нет, поэтому функция существует для абсолютно любых значений переменной х, кроме нуля.
Если подставить вместо переменной х ее противоположное значение —х, то получим, что функция является нечетной, т.е. ее график будет симметричным относительно точки начала координат:

$y\left(-x\right)=\frac{12}{-x}=-\frac{12}{x}=-y\left(x\right)$

Найдем точки графика, подставив для этого в уравнение функции любые значения для переменной х.

$x=-12$

$y\left(-12\right)=\frac{12}{-12}=-1$

Точка (—12; —1)

$x=-6$

$y\left(-6\right)=\frac{12}{-6}=-2$

Точка (—6; —2)

$x=-4$

$y\left(-4\right)=\frac{12}{-4}=-3$

Точка (—4; —3)

$x=-3$

$y\left(-3\right)=\frac{12}{-3}=-4$

Точка (—3; —4)

$x=-2$

$y\left(-2\right)=\frac{12}{-2}=-6$

Точка (—2; —6)

$x=-1$

$y\left(-1\right)=\frac{12}{-1}=-12$

Точка (—1; —12)
Найденных точек достаточно для построения одной части графика. Другую же часть построим симметрично началу координат, вследствие нечетности функции.

Постройте график функции y=12/x

Пожалуйста, зарегистрируйтесь или войдите, чтобы добавить ответ.