Законы движения материальной точки
Кинематические законы движения
Механическим движением называют изменение положения тела относительно тел, составляющих систему отсчета. Для того чтобы описать движение тела следует выбрать систему отсчета в которую ходят: тело отсчёта, система координат, которая связана с телом отсчета и часы (отсчет времени). Движение можно описать при помощи трех способов: координатного (скалярного), векторного, траекторного (натурального).
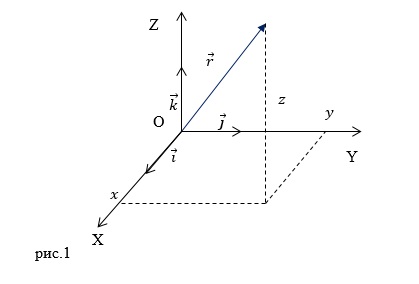
В декартовой системе координат (рис.1) положение материальной точки (M) определяют три координаты (![]() ) или радиус-вектор
) или радиус-вектор ![]() , который проведен из начала системы координат в рассматриваемую точку.
, который проведен из начала системы координат в рассматриваемую точку.
Если точка перемещается, то в любой следующий момент времени координаты изменяются:
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{c} x=x\left(t\right), \\ y=y\left(t\right), \\ z=z\left(t\right). \end{array} \right.(1)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1fa0f2bebb8960f38b31cbff151c8a5c_l3.png)
Уравнения (1) называют скалярными кинематическими уравнениями движения материальной точки (параметрическими уравнениями). Данные уравнения определяют перемещение точки координатным способом.
Радиус- вектор можно определить как:
![]()
где ![]() ,
, ![]() ,
, ![]() — единичные векторы по осям X,Y,Z (рис.1).Выражение:
— единичные векторы по осям X,Y,Z (рис.1).Выражение:
![]()
является векторным кинематическим уравнением движения материальной точки. Выражения 1-3 называют кинематическими законами движения материальной точки. Данные законы полностью описывают движение точки.
Модуль (длина) радиус- вектора ![]() находится при помощи формулы:
находится при помощи формулы:
![]()
Динамические законы движения материальной точки
Динамика рассматривает движение материальной точки в зависимости от сил, которые к ней приложены. Основные законы классической динамики сформулированы Ньютоном.
Первый закон Ньютона:
Материальная точка не изменяет своего состояния покоя или движется равномерно и прямолинейно, если внешние силы на нее не действуют или действие их взаимно скомпенсированы.
Второй закон Ньютона:
В инерциальных системах отсчета результирующая сил (![]() ), приложенных к материальной точке равна произведению ее массы (
), приложенных к материальной точке равна произведению ее массы (![]() ) на ускорение (
) на ускорение (![]() ):
):
![]()
Дифференциальные уравнения движения материальной точки записываю как:
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{c} m\frac{d^2x}{dt^2}=\sum{F_{ix},} \\ m\frac{d^2y}{dt^2}=\sum{F_{iy},} \\ m\frac{d^2z}{dt^2}=\sum{F_{iz}} \end{array} \right.\left(6\right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d18a39afde7069b202569a1ca30dc689_l3.png)
где ![]() — координаты перемещающейся материальной точки,
— координаты перемещающейся материальной точки, ![]() ,
, ![]() ,
, ![]() —проекции сил, приложенных к точке.
—проекции сил, приложенных к точке.
С помощью дифференциальных уравнений перемещения материальной точки при известной массе находят силы, которые действуют на точку.
Примеры решения задач
| Задание | На материальную точку действуют сила тяжести (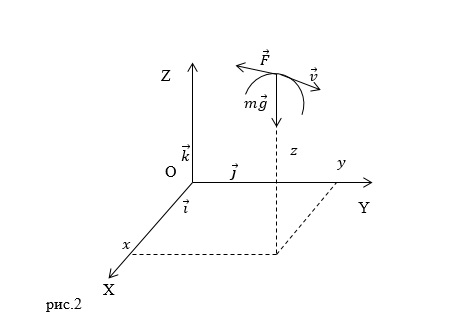
|
| Решение | Проекциями векторного равенства На ось X: на ось Y: на ось Z: Применяя второй закон Ньютона выражения (1.1) — (1.3) преобразуем к виду: |
| Ответ | 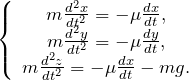 |
| Задание | Радиус — вектор материальной точки задан функцией: |
| Решение | Векторное кинематическое уравнение имеет вид:
В условии задачи радиус 0 вектор задан как: Следовательно, сравнивая выражения (2.1) и (2.2) имеем: Выразим из первого уравнения (2.3) время и подставим его во второе уравнение, получим: Уравнение траектории — это парабола (рис.3). 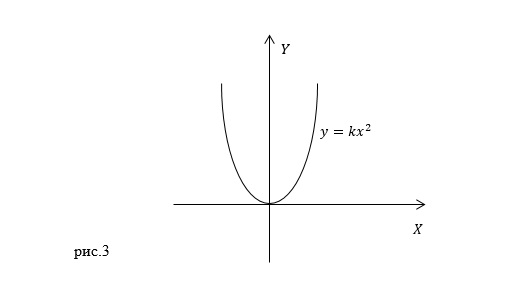
|
| Ответ |






![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{c} m\frac{d^2x}{dt^2}=-\mu \frac{dx}{dt}, \\ m\frac{d^2y}{dt^2}=-\mu \frac{dy}{dt}, \\ m\frac{d^2z}{dt^2}=-\mu \frac{dx}{dt}-mg. \end{array} \right.\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6af206f8043b9d52cdacedf793196e92_l3.png)





