Векторы в пространстве
Основные понятия и определения векторов в пространстве
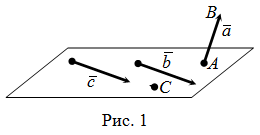
Если начало вектора совпадает с его концом, то такой вектор называется нулевым и обозначается как ![]() . (На рисунке 1 нулевым является вектор
. (На рисунке 1 нулевым является вектор ![]() .)
.)
Замечание. Любая точка пространства рассматривается как нулевой вектор.
Длиной или модулем ![]() вектора
вектора ![]() называется длина отрезка
называется длина отрезка ![]() .
.
Замечание. Длина нулевого вектора равна нулю:
![]()
Вектор, длина которого равна единице, называется единичным.
Коллинеарные и неколлинеарные векторы в пространстве
Два ненулевых вектора называются коллинеарными или параллельными, если они лежат на одной или на параллельных прямых. (На рисунке 1 таковыми являются векторы ![]() и
и ![]() .)
.)
Лемма. Если два ненулевых вектора ![]() и
и ![]() коллинеарны, то существует такое число
коллинеарны, то существует такое число ![]() , что имеет место равенство:
, что имеет место равенство:
![]()
Сонаправленные и противоположные векторы в пространстве
Два ненулевых коллинеарных вектора ![]() и
и ![]() называются сонаправленными, если их направления совпадают (
называются сонаправленными, если их направления совпадают (![]() ); и противоположно направленными – в противном случае (
); и противоположно направленными – в противном случае (![]() ).
).
Векторы ![]() и
и ![]() называются равными, если они сонаправленны и их длины равны.
называются равными, если они сонаправленны и их длины равны.
Утверждение. От любой точки пространства можно отложить вектор, равный данному, и притом только один.
Два ненулевых вектора ![]() и
и ![]() называются противоположными, если их длины равны и они противоположно направлены.
называются противоположными, если их длины равны и они противоположно направлены.
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
Замечание. Любые два коллинеарных вектора компланарны; три вектора, среди которых имеется два коллинеарных, также компланарны.
Утверждение. Если вектор ![]() можно представить в виде линейной комбинации векторов
можно представить в виде линейной комбинации векторов ![]() и
и ![]() :
:
![]()
то векторы ![]() и
и ![]() компланарны.
компланарны.
![]()
Если точки ![]() и
и ![]() заданы в пространстве своими координатами:
заданы в пространстве своими координатами: ![]() , то для нахождения координат вектора
, то для нахождения координат вектора ![]() необходимо от координат конца точки
необходимо от координат конца точки ![]() этого вектора отнять соответствующие координаты начала точки
этого вектора отнять соответствующие координаты начала точки ![]() :
:
![]()
Примеры решения задач
| Задание | Найти координаты вектора |
| Решение |
Для нахождения координат вектора от координат его конца отнимем соответствующие координаты начала:
|
| Ответ | |
Если вектор ![]() задан в пространстве своими координатами:
задан в пространстве своими координатами: ![]() , то его длина равна корню квадратному из суммы квадратов координат:
, то его длина равна корню квадратному из суммы квадратов координат:
![]()
| Задание | Найти модуль вектора |
| Решение |
Модуль вектора равен корню квадратному из суммы квадратов его координат, то есть для заданного вектора |
| Ответ | |











