Векторное произведение векторов

Определение и формула векторного произведения векторов

ОПРЕДЕЛЕНИЕ

Векторным произведением $\left[\bar{a},\; \bar{b}\right]=\bar{a}\times \bar{b}$ двух векторов $\bar{a}$ и $\bar{b}$ называется вектор $\bar{c}$ , перпендикулярный к плоскости этих векторов и направленный так, что наименьший поворот от вектора $\bar{a}$ к вектору $\bar{b}$ происходит против хода часовой стрелки, если смотреть с конца вектора $\bar{c}$ (рис. 1), причем

$\left|\bar{c}\right|=\left|\bar{a}\right|\cdot \left|\bar{b}\right|\cdot \sin \left(\mathop{\bar{a},\; \bar{b}}\limits^{\wedge } \right)$

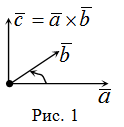
Если векторы $\bar{a}$ и $\bar{b}$ заданы своими координатами: $\bar{a}=\left(a_{1} ;\; a_{2} ;\; a_{3} \right),\ \bar{b}=\left(b_{1} ;\; b_{2} ;\; b_{3} \right)$ , то их векторное произведение вычисляется по формуле:

$\left[\bar{a},\; \bar{b}\right]=\bar{a}\times \bar{b}=\left|\begin{array}{ccc} \bar{i} & \bar{j} & \bar{k} \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{array}\right|,$

где $\bar{i},\; \bar{j},\; \bar{k}$ – орты координатных осей $Ox,\; Oy,\; Oz$ соответственно.

Если раскрыть этот определитель по первой строке:

$\left[\bar{a},\; \bar{b}\right]=\bar{a}\times \bar{b}=\left|\begin{array}{ccc} \bar{i} & \bar{j} & \bar{k} \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{array}\right|\begin{array}{c} {\leftarrow } \\ {} \\ {} \end{array}=\bar{i}\cdot \left|\begin{array}{cc} a_{2} & a_{3} \\ b_{2} & b_{3} \end{array}\right|-\bar{j}\cdot \left|\begin{array}{cc} a_{1} & a_{3} \\ b_{1} & b_{3} \end{array}\right|+\bar{k}\cdot \left|\begin{array}{cc} a_{1} & a_{2} \\ b_{1} & b_{2} \end{array}\right|=$

$=\bar{i}\cdot \left(a_{2} b_{3} -a_{3} b_{2} \right)-\bar{j}\cdot \left(a_{1} b_{3} -a_{3} b_{1} \right)+\bar{k}\cdot \left(a_{1} b_{2} -a_{2} b_{1} \right),$

то получаем, что

$\bar{c}=\left[\bar{a},\; \bar{b}\right]=\left(a_{2} b_{3} -a_{3} b_{2} ;\; a_{1} b_{3} -a_{3} b_{1} ;\; a_{1} b_{2} -a_{2} b_{1} \right)$

ПРИМЕР

Задание

Найти векторное произведение векторов $\bar{a}=\left(-1;\; 1;\; 2\right)$ и $\bar{b}=\left(0;\; 1;\; -1\right)$

Решение

Для нахождения векторного произведения составим определитель, в первой строке которого записаны орты $\bar{i},\; \bar{j},\; \bar{k}$ координатных осей, а во второй и третьей строках координаты векторов $\bar{a}$ и $\bar{b}$ соответственно:

$\left[\bar{a},\; \bar{b}\right]=\left|\begin{array}{ccc} \bar{i} & \bar{j} & \bar{k} \\ -1 & 1 & 2 \\ 0 & 1 & -1 \end{array}\right|$

Вычислим этот определитель, разложив его по элементам первой строки:

$\left[\bar{a},\; \bar{b}\right]=\left|\begin{array}{ccc} \bar{i} & \bar{j} & \bar{k} \\ -1 & 1 & 2 \\ 0 & 1 & -1 \end{array}\right|\begin{array}{c} {\leftarrow } \\ {} \\ {} \end{array}=\bar{i}\cdot \left|\begin{array}{cc} 1 & 2 \\ 1 & -1 \end{array}\right|-\bar{j}\cdot \left|\begin{array}{cc} -1 & 2 \\ 0 & -1 \end{array}\right|+\bar{k}\cdot \left|\begin{array}{cc} -1 & 1 \\ 0 & 1 \end{array}\right|=$

$=\bar{i}\cdot \left(-1-2\right)-\bar{j}\cdot \left(1-0\right)+\bar{k}\cdot \left(-1-0\right)=-3\bar{i}-\bar{j}-\bar{k}=\left(-3;\; -1;\; -1\right)$

Ответ

$\left[\bar{a},\; \bar{b}\right]=\left(-3;\; -1;\; -1\right)$

Свойства векторного произведения векторов

1. Геометрический смысл векторного произведения. Модуль векторного произведения двух векторов $\bar{a}$ и $\bar{b}$ равен площади параллелограмма построенного на этих векторах:

$S_{parall} =\left|\bar{a}\times \bar{b}\right|$

ЗАМЕЧАНИЕ

Площадь треугольника построенного на векторах $\bar{a}$ и $\bar{b}$ равна половине модуля векторного произведения указанных векторов:

$S_{\Delta } =\frac{1}{2} \left|\bar{a}\times \bar{b}\right|$

2. Векторное произведение двух ненулевых векторов $\bar{a}$ и $\bar{b}$ равно нулю тогда и только тогда, когда эти векторы коллинеарны.

3. $\left[\bar{a},\; \bar{b}\right]=-\left[\bar{b},\; \bar{a}\right]$ .

4. $\left[\lambda \bar{a},\; \bar{b}\right]=\left[\bar{a},\; \lambda \bar{b}\right]=\lambda \cdot \left[\bar{a},\; \bar{b}\right]$ .

5. $\left[\bar{a}+\bar{b},\; \bar{c}\right]=\left[\bar{a},\; \bar{c}\right]+\left[\bar{b},\; \bar{c}\right]$ .

ПРИМЕР

Задание	Найти площадь треугольника, образованного векторами $\bar{a}$ и $\bar{b}$ , если известно, что $\left\|\bar{a}\right\|=2,\ \left\|\bar{b}\right\|=3$ , а угол между этими векторами $\left(\mathop{\bar{a},\; \bar{b}}\limits^{\wedge } \right)=30^{\circ }$ .
Решение	Известно, что площадь треугольника, построенного на двух векторах, равна половине длины вектора, который есть их векторным произведением. Модуль векторного произведения векторов $\bar{a}$ и $\bar{b}$ равен произведению модулей этих векторов на синус угла между ними. То есть имеем: $S_{\Delta } =\frac{1}{2} \left\|\bar{a}\times \bar{b}\right\|=\frac{\left\|\bar{a}\right\|\cdot \left\|\bar{b}\right\|\cdot \sin \left(\mathop{\bar{a},\; \bar{b}}\limits^{\wedge } \right)}{2} =\frac{2\cdot 3\cdot \sin 30^{\circ } }{2} =3\cdot \frac{1}{2} =\frac{3}{2}$ (кв. ед.).
Ответ	$S_{\Delta } =\frac{3}{2}$ (кв. ед.)

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Векторное произведение векторов

Определение и формула векторного произведения векторов

Свойства векторного произведения векторов