Линейные операции над векторами

Рассмотрим два ненулевых вектора $\bar{a}$ и $\bar{b}$ .

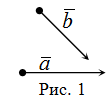
1. Сложение (сумма) векторов

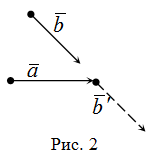
Замечание. Если начало вектора $\bar{b}$ не совпадает с концом вектора $\bar{a}$ , то от конца вектора $\bar{a}$ надо отложить вектор $\bar{b}'$ , равный вектору $\bar{b}$ (рис. 2).

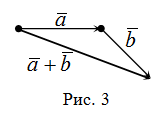
Правило треугольника сложения векторов. Если конец вектора $\bar{a}$ совпадает с началом вектора $\bar{b}$ , то суммой этих векторов есть вектор, начало которого совпадает с началом вектора $\bar{a}$ , а конец – с концом вектора $\bar{b}$ (рис. 3).

Правило треугольника сложения векторов. рис 3

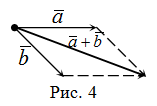
Правило треугольника сложения векторов. рис 4

Правило параллелограмма сложения векторов. Если два неколлинеарных вектора $\bar{a}$ и $\bar{b}$ имеют общее начало (рис. 4), то суммой этих вектор есть вектор, имеющий общее начало с указанными векторами и совпадающий с диагональю параллелограмма, построенного на этих векторах $\bar{a}$ и $\bar{b}$ .

Сложение векторов обладают переместительным и распределительным свойствами:

$\bar{a}+\bar{b}=\bar{b}+\bar{a}, \left(\bar{a}+\bar{b}\right)+\bar{c}=\bar{a}+\left(\bar{b}+\bar{c}\right)$

ТЕОРЕМА

Для любых точек $A,\; B,\; C$ имеет место векторное равенство

$\overline{AB}+\overline{BC}=\overline{AC}$

Если векторы $\bar{a}$ и $\bar{b}$ заданы своими координатами, например, на плоскости, $\bar{a}=\left(a_{1} ;\; a_{2} \right),\ \bar{b}=\left(b_{1} ;\; b_{2} \right)$ , тогда суммой этих векторов есть вектор $\bar{c}$ , координаты которого равны сумме соответствующих координат векторов-слагаемых:

$\bar{c}=\bar{a}+\bar{b}=\left(a_{1} ;\; a_{2} \right)+\left(b_{1} ;\; b_{2} \right)=\left(a_{1} +b_{1} ;\; a_{2} +b_{2} \right)$

ПРИМЕР

Задание	Найти сумму векторов $\bar{a}=\left(-1;\; 0;\; 2\right)$ и $\bar{b}=\left(1;\; -3;\; 1\right)$
Решение	Суммой заданных векторов будет вектор, координаты которого равны сумме соответствующих координат векторов $\bar{a}$ и $\bar{b}$ : $\bar{a}+\bar{b}=\left(-1;\; 0;\; 2\right)+\left(1;\; -3;\; 1\right)=\left(-1+1;\; 0+\left(-3\right)\, ;\; 2+1\right)=\left(0;\; -3;\; 3\right)$
Ответ	$\bar{a}+\bar{b}=\left(0;\; -3;\; 3\right)$

2. Разность векторов

Противоположным вектором $-\bar{a}$ к некоторому вектору $\bar{a}$ называется вектор, противоположно направленный данному и имеющий такую же длину.

Замечание. Сумма противоположных векторов равна нулевому вектору:

$\bar{a}+\left(-\bar{a}\right)=\bar{0}$

Разностью $\bar{a}-\bar{b}$ двух векторов $\bar{a}$ и $\bar{b}$ называется сумма вектора $\bar{a}$ и вектора $-\bar{b}$ , который является противоположным вектору $\bar{b}$ :

$\bar{a}-\bar{b}=\bar{a}+\left(-\bar{b}\right)$

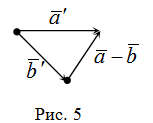
Чтобы построить геометрически разность векторов $\bar{a}$ и $\bar{b}$ , необходимо совместить начала этих векторов (то есть от одной точки отложить равные им векторы $\bar{a}'$ и $\bar{b}'$ ), тогда вектор, начало которого совпадает с концом вектора $\bar{b}'$ , а конец – с концом вектора $\bar{a}'$ , и будет искомой разностью $\bar{a}-\bar{b}$ (рис. 5).

ТЕОРЕМА

Для векторов $\overline{AB}$ и $\overline{AC}$ , имеющих общее начало, имеет место векторное равенство:

$\overline{AC}-\overline{AB}=\overline{BC}$

Если векторы $\bar{a}$ и $\bar{b}$ заданы своими координатами: $\bar{a}=\left(a_{1} ;\; a_{2} \right),\ \bar{b}=\left(b_{1} ;\; b_{2} \right)$ , то их разностью есть вектор $\bar{c}$ , координаты которого равны разности соответствующих координат векторов $\bar{a}$ и $\bar{b}$ :

$\bar{c}=\bar{a}-\bar{b}=\left(a_{1} ;\; a_{2} \right)-\left(b_{1} ;\; b_{2} \right)=\left(a_{1} -b_{1} ;\; a_{2} -b_{2} \right)$

ПРИМЕР

Задание	Найти разность векторов $\bar{a}=\left(1;\; -7\right)$ и $\bar{b}=\left(-1;\; 2\right)$
Решение	Чтобы найти вектор-разность необходимо от координат вектора $\bar{a}$ отнять соответствующие координаты вектора $\bar{b}$ , то есть $\bar{a}-\bar{b}=\left(1;\; -7\right)-\left(-1;\; 2\right)=\left(1-\left(-1\right)\, ;\; -7-2\right)=\left(2;\; -9\right)$
Ответ	$\bar{a}-\bar{b}=\left(2;\; -9\right)$

3. Умножение вектора на число

Произведением вектора $\bar{a}$ на число $\lambda \ne 0$ называется вектор $\bar{b}=\lambda \bar{a}$ , модуль которого $\left|\bar{b}\right|=\left|\lambda \right|\cdot \left|\bar{a}\right|$ , причем вектор $\bar{b}$ будет сонаправлен с вектором $\bar{a}$ , если $\lambda >0$ , и противоположно направлен в случае, если $\lambda <0$ .

Произведением вектора $\bar{a}=\left(a_{1} ;\; a_{2} \right)$ на число $\lambda \ne 0$ называется вектор, полученный из исходного умножением его каждой координаты на число $\lambda$ :

$\lambda \bar{a}=\lambda \cdot \left(a_{1} ;\; a_{2} \right)=\left(\lambda \cdot a_{1} ;\; \lambda \cdot a_{2} \right)=\left(\lambda a_{1} ;\; \lambda a_{2} \right)$

ПРИМЕР

Задание	Известно, что вектор $\bar{a}=\left(2;\; 3\right)$ . Найти вектор $2\bar{a}$ .
Решение	Чтобы найти нужный вектор, умножим каждую координату исходного вектора $\bar{a}$ на число $\lambda =2$ : $2\bar{a}=2\cdot \left(2;\; 3\right)=\left(2\cdot 2;\; 2\cdot 3\right)=\left(4;\; 6\right)$
Ответ	$2\bar{a}=\left(4;\; 6\right)$ .

ТЕОРЕМА

Два ненулевых вектора $\bar{a}$ и $\bar{b}$ коллинеарны тогда и только тогда, когда существует такое число $\lambda \ne 0$ , что имеет место равенство: $\bar{a}=\lambda \bar{b}$ .

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Линейные операции над векторами

1. Сложение (сумма) векторов

2. Разность векторов

3. Умножение вектора на число