Уравнение Фурье

Формула и применение уравнения Фурье

Уравнение Фурье использует аппарат весьма абстрактной дисциплины – математической физики. На практике же оно применяется для изучения процессов теплопроводности разных тел. Это дифференциальное уравнение в частных производных позволяет узнать, насколько быстро изменяется температура тела, к которому подвели теплоту.

Однако до того как было получено уравнение Фурье, для него была построена математическая модель и выдвинута соответствующая гипотеза.

Мы рассматриваем стержень из однородного материала, для которого известна теплопроводность $\lambda$ . Будем считать, что стержень тонкий – настолько, что температура во всех точках каждого поперечного сечения одинакова. Стержень теплоизолирован от внешней среды, и теплота подводится и распространяется только вдоль оси Ох – вдоль стержня.

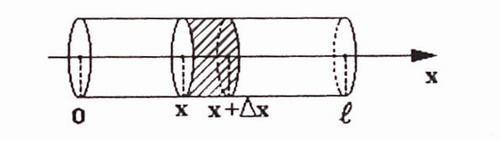
Для этого случая существует гипотеза (или закон) Фурье, связывающий количество подведенной теплоты, изменение температуры стержня во времени, геометрические и физические характеристики стержня:

$d^2 Q=-\lambda \cdot \frac{\partial t}{\partial n} \cdot dF \cdot d\tau$

Физический смысл гипотезы более понятен, если некоторые множители из правой части перенести в левую:

$\frac{d^2 Q}{dF \cdot d\tau} =-\lambda \cdot \frac{\partial t}{\partial n}$

Количество теплоты $d^2 Q$ , подведенное к элементу поверхности $dF$ за отрезок времени $d\tau$ пропорционально градиенту температуры $\frac{\partial t}{\partial n}$ . Температурный градиент – это, по сути, изменение температуры на отрезке стержня $\partial n$ . Используется обозначение n (нормаль), а не х, чтобы указать: температура распространяется перпендикулярно изотермическим поверхностям поперечного сечения. Коэффициент пропорциональности $\lambda$ – это коэффициент теплопроводности стержня. Знак «минус» означает, что теплота передается в направлении снижения температуры.

С другой стороны, количество подведенной теплоты, подведенное к участку стержня длиной dx, чтобы его температура возросла на dt:

$d^2 Q=c\rho \cdot dF \cdot dx \cdot dt$

Здесь с – теплоемкость стержня, $\rho$ – плотность.

С использованием этой гипотезы и было получено уравнение Фурье:

$\frac{\partial u}{\partial t} =a\Delta u$

Здесь переменная u – температура (обозначена буквой, традиционной в матфизике), t – время, $\Delta$ – оператор Лапласа:

$\Delta =\frac{\partial^2}{\partial x^2} +\frac{\partial^2}{\partial y^2} +\frac{\partial^2}{\partial z^2}$

Если задача одномерная (а в случае со стержнем так оно и есть), уравнение Фурье примет вид:

$\frac{\partial u}{\partial t} =a\frac{\partial^2 u}{\partial x^2}$

Чтобы решить это уравнение, нужно задать граничные условия (температура на концах стержней в какой-то момент времени) и начальные условия (распределение температур по стержню в начальный момент времени).

Примеры решения задач

ПРИМЕР 1

Задание

Задана бесконечно большая плоская стенка толщиной $\delta$ . Теплопроводность стенки $\lambda$ . Температурное распределение в стенке не изменяется. Температуры на границах: $t_1,\ t_2$ . Найти закон изменения температуры по толщине стенки.

Решение

Так как теплота распространяется только вдоль одной оси, запишем уравнение Фурье:

$\frac{\partial u}{\partial t} =a\frac{\partial^2 u}{\partial x^2}$

Так как распределение температур в стенке уже установилось:

$\frac{\partial^2 u}{\partial x^2} =0$

Интегрируем это выражение:

$\frac{\partial u}{\partial x} =C_1$

$u=C_1 x+C_2$

Используем граничные условия: $u (x = 0) = t_1,\ u (x = \delta ) = t_2$ .

$\left\{\begin{array}{l} {t_1 =C_1 \cdot 0+C_2} \\ {t_2 =C_1 \cdot \delta +C_2} \end{array}\right$

Выразив постоянные интегрирования, получим закон изменения температуры:

$u= \frac{t_2 -t_1}{\delta} x+t_1$

Ответ

$u= \frac{t_2 -t_1}{\delta} x+t_1$

ПРИМЕР 2

Задание

Рассчитать закон изменения температуры в стекле и тепловые потери из помещения через стекло за 1 час, если температура внутри помещения $20^{\circ}\ C$ , температура на улице $-5^{\circ}\ C$ , теплопроводность стекла $\lambda = 0,8$ Вт/(м•К), толщина стекла 8 мм, площадь остекления 20 м $^{2}$ .

Решение

Считаем, что распределение температур стационарно. Размеры стекла достаточно большие, чтобы игнорировать их конечность. Используем уравнение Фурье для одномерного случая:

$\frac{\partial u}{\partial t} =a\frac{\partial^2 u}{\partial x^2}$

Так как поле температур стационарно:

$\frac{\partial^2 u}{\partial x^2} =0$

Дважды проинтегрировав, получим:

$u=C_1 x+C_2$

Подставим граничные условия: u (x = 0 м) = $20^{\circ}\ C$ , u (x = 0,008 м) = $-5^{\circ}\ C$ .

$\left\{\begin{array}{l} {20=C_1 \cdot 0+C_2} \\ {-5=C_1 \cdot 0,008+C_2} \end{array}\right$

Закон изменения температуры по толщине стекла:

$u= -3125x+20$

Воспользуемся гипотезой Фурье, чтобы вычислить потери теплоты:

$d^2 Q=-\lambda \cdot \frac{\partial t}{\partial n} \cdot dF \cdot d\tau$

$Q=\lambda \cdot \frac{\Delta t}{\delta} \cdot F\cdot \tau =0,8 \cdot \frac{25}{0,008} \cdot 20\cdot 3600=225\cdot 10^6\ J$

Ответ

$u= -3125x+20,\ Q = 225\cdot 10^6$ Дж

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Уравнение Фурье

Формула и применение уравнения Фурье

Примеры решения задач