Уравнение бегущей волны
Теория про уравнение бегущей волны
Когда мы говорим о движении тела, то имеем в виду перемещение в пространстве его самого. В случае же волнового движения речь идет не о перемещении среды или поля, а о перемещении возбужденного состояния среды или поля. В волне определенное состояние, сначала локализованное в одном месте пространства, передается (перемещается) в другие, соседние точки пространства.
Состояние среды или поля в данной точке пространства характеризуется одним или несколькими параметрами. Такими параметрами, например, в волне, образуемой на струне, является отклонение данного участка струны от положения равновесия (х), в звуковой волне в воздухе — это величина, характеризующая сжатие или расширение воздуха, в электромагнитной волне — это модули векторов ![]() и
и ![]() . Важнейшим понятием для любой волны является фаза. Под фазой понимается состояние волны в данной точке и в данный момент времени, описанное соответствующими параметрами. Например, фаза электромагнитной волны задается модулями векторов
. Важнейшим понятием для любой волны является фаза. Под фазой понимается состояние волны в данной точке и в данный момент времени, описанное соответствующими параметрами. Например, фаза электромагнитной волны задается модулями векторов ![]() и
и ![]() . Фаза от точки к точке меняется. Таким обpазом, фаза волны в математическом смысле есть функция координат и времени. С понятием фазы связано понятие волновой поверхности. Это поверхность, все точки которой в данный момент времени находятся в одной и той же фазе, т.е. это поверхность постоянной фазы.
. Фаза от точки к точке меняется. Таким обpазом, фаза волны в математическом смысле есть функция координат и времени. С понятием фазы связано понятие волновой поверхности. Это поверхность, все точки которой в данный момент времени находятся в одной и той же фазе, т.е. это поверхность постоянной фазы.
Понятия волновой поверхности и фазы позволяют провести некоторую классификацию волн по характеру их поведения в пространстве и времени. Если волновые поверхности перемещаются в пространстве (например, обычные волны на поверхности воды), то волна называется бегущей.
Бегущие волны можно разделить на: плоские, сферические и цилиндрические.
Уравнение бегущей плоской волны
Уравнение плоской гармонической волны – это выражение вида:
![]()
или (что одно и то же)
![]()
где под x можно подразумевать любой параметр, характеризующий состояние среды (например, величину давления, температуру и т.д.); A- амплитуда волны; w- циклическая частота; r-расстояние от источника, возбуждающего волну, до точки пространства, в которой рассматривается изменение некоторого свойства среды, ![]() – скорость волны;
– скорость волны; ![]() — начальная фаза волны (выбирается началом отсчета). Причем
— начальная фаза волны (выбирается началом отсчета). Причем ![]() отличаются сдвигом на
отличаются сдвигом на ![]() — волновое число;
— волновое число; ![]() — длина волны; выражение
— длина волны; выражение ![]() называется фазой волны.
называется фазой волны.
Экспоненциальная форма записи уравнения бегущей волны
Экспоненциальная форма записи уравнения (1) имеет вид:
![]()
где ![]() – радиус вектор, проведенный в рассматриваемую току среды;
– радиус вектор, проведенный в рассматриваемую току среды; ![]() – волновой вектор;
– волновой вектор; ![]() — единичный вектор, указывающий направление волны,
— единичный вектор, указывающий направление волны, ![]() — комплексная амплитуда.
— комплексная амплитуда.
Для уравнения (2) необходимо отметить, что такая форма записи удобна для дифференцирования волновых уравнений. Однако физический смысл имеет только вещественная часть экспоненциального выражения.
Уравнение сферической и цилиндрической бегущей волны
Уравнение сферической бегущей волны:
![]()
В экспоненциальной форме уравнение сферической волны имеет вид:
![]()
где ![]() – комплексная амплитуда. Везде, кроме особой точки r=0, функция x удовлетворяет волновому уравнению
– комплексная амплитуда. Везде, кроме особой точки r=0, функция x удовлетворяет волновому уравнению ![]() .
.
Уравнение цилиндрическое бегущей волны:
![]()
где r – расстояние от оси.
![]()
где ![]() – комплексная амплитуда.
– комплексная амплитуда.
Примеры решения задач
| Задание | Плоская незатухающая звуковая волна возбуждается источником колебаний частоты |
| Решение | Запишем уравнение бегущей волны, зная, что она плоская:
Используем в записи уравнения w= Из условий задачи известно, что в начальный момент смещение точек источника максимально. Следовательно, Получим: Соответственно: |
| Ответ |
| Задание | На рисунке дан график смещений 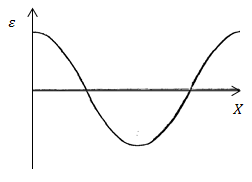
|
| Решение | На рисунке дана «моментальная фотография» смещения частиц в бегущей волне
Исходя из рисунка волну можно описать уравнением в некоторый момент t: В случае продольной плоской волны плотность энергии выражается как: где подставляя (2.1) в (2.3), а затем в (2.2), получаем:
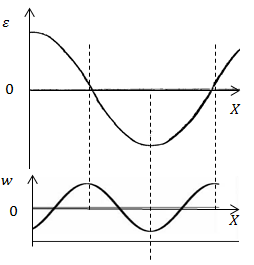
|











