Стационарное уравнение Шредингера

Уравнение Шредингера

Для частиц квантового мира действуют другие законы, чем для объектов классической механики. Согласно предположению де Бройля, микрообъекты обладают свойствами и частицы, и волны – и, действительно, при рассеивании пучка электронов на отверстии наблюдается дифракция, характерная для волн.

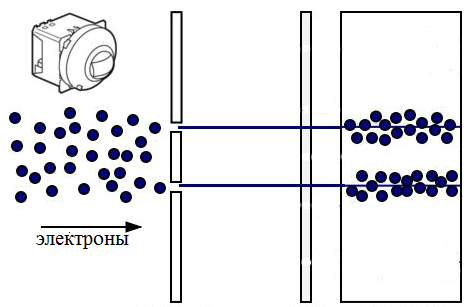
Поэтому можно говорить не о траекториях движения квантовых частиц, а о вероятности того, что частица будет находиться в конкретной точке в некий момент времени.

Что описывает уравнение Шредингера

Уравнение Шрёдингера предназначено для описания особенностей движения квантовых объектов в полях внешних сил. Зачастую частица передвигается сквозь силовое поле, не зависящее от времени. Для этого случая записывается стационарное уравнение Шрёдингера:

$\Delta \psi +\frac{2m}{\hbar ^2 } (E-U)\psi =0$

В представленном уравнении m и Е – масса и соответственно энергия частицы, пребывающей в силовом поле, а U – потенциальная энергия этого поля. $\Delta = \frac{\partial ^2 }{\partial x^2 } +\frac{\partial ^2 }{\partial y^2 } +\frac{\partial ^2 }{\partial z^2 }$ — оператор Лапласа. $\hbar$ — постоянная Планка, равная 6,626•10^-34Дж•с.

$\psi$ (её также называют амплитудой вероятности, или пси-функцией) – это и есть функция, позволяющая узнать, в каком месте пространства, скорее всего, будет находиться наш микрообъект. Физический смысл имеет не сама функция, а её квадрат. Вероятность того, что частица находится в элементарном объеме $dV$ :

$dW=\left|\psi \right|^2 dV$

Следовательно, найти функцию в конечном объеме можно с вероятностью:

$W=\int _{V}\left|\psi \right|^2 dV$

Так как пси-функция – вероятность, то она не может быть ни меньше нуля, ни превышать единицу. Полная вероятность найти частицу в бесконечном объеме – это условие нормировки:

$\int _{-\infty }^{\infty }\left|\psi \right|^2 dV=1$

Для пси-функции работает принцип суперпозиции: если частица или система может находиться в ряде квантовых состояний $\psi _1,\ \psi _2 \dots \psi _{n}$ , то для нее возможно и состояние, определяемое их суммой:

$\psi =\psi _1 +\psi _2 +...+\psi _{n}$

Стационарное уравнение Шрёдингера имеет множество решений, однако при решении следует учесть граничные условия и отобрать только собственные решения – те, которые обладают физическим смыслом. Такие решения существуют только для отдельных значений энергии частицы Е, которые и образуют дискретный энергетический спектр частицы.

Примеры решения задач

ПРИМЕР 1

Задание

Волновая функция описывает расстояние электрона до ядра водорода: $\psi =Ae ^{-\frac{r}{A} } .$ r – расстояние между электроном и ядром, a – первый Боровский радиус. На каком расстоянии от ядра электрон, скорее всего, находится?

Решение

1) Выразив объем через радиус ядра, найдем вероятность того, что электрон находится в пределах некоторого расстояния от ядра:

$dW=\left|\psi \right|^2 dV=4\pi r ^2 \left|\psi \right|^2 dr= 4\pi r ^2 A^2 e^{-\frac{2r }{A} } dr$

2) Вероятность того, что электрон находится в пределах элементарного «кольца» dr:

$\omega =\frac{dW}{dr} =4\pi r ^2 A^2 e^{-\frac{2r }{A} }$

3) Чтобы найти наиболее вероятное расстояние, найдем экстремум из последнего выражения:

$\frac{d\omega }{dr } =(4\pi r ^2 A^2 e^{-\frac{2r }{A} } )'=8\pi rA ^2 e^{-\frac{2r }{A} } +4\pi r ^2 A^2 e^{-\frac{2r }{A} } (-\frac{2}{a} )$

$\frac{d\omega }{dr } =0$

Решив это уравнение, получим r = a – самое вероятное расстояние между электроном и ядром.

Ответ

r = a – с наибольшей вероятностью ядро находится на расстоянии первого Боровского радиуса от ядра.

ПРИМЕР 2

Задание

Найти уровни энергии частицы в бесконечно глубокой потенциальной яме.

Решение

Пусть частица движется по оси абсцисс. Ширина ямы – l. Энергию мы отсчитываем от дна ямы и описываем функцией:

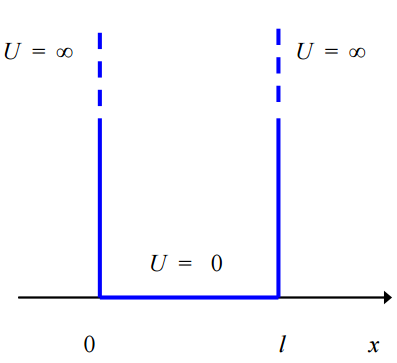
Запишем одномерное стационарное уравнение Шрёдингера:

$\Delta \psi +\frac{2m}{\hbar ^2 } (E-U)\psi =0$

Рассмотрим граничные условия. Так как мы считаем, что частица не может проникнуть за стенки, то за пределами ямы $\psi$ =0. На границе ямы пси-функция также равна нулю: $\psi (0)=\psi (l)=0.$ В яме потенциальная энергия U=0.