Упрощение тригонометрических выражений

При упрощении тригонометрических выражений используются свойства тригонометрических функций и тригонометрические формулы.

Основные тригонометрические формулы

Соотношения между тригонометрическими функциями одного аргумента

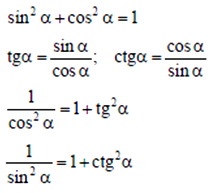
Тригонометрические функции суммы и разности углов

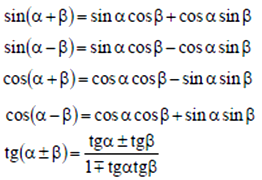
Тригонометрические функции двойного и тройного аргументов

Формулы понижения степени

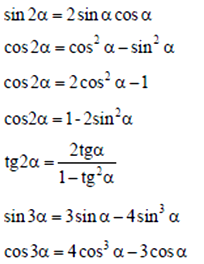
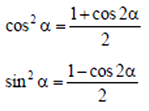
Тригонометрические функции половинного аргумента

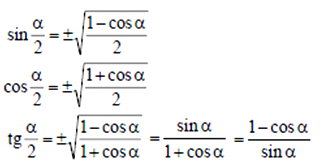
Формулы преобразования произведения тригонометрических функций в сумму

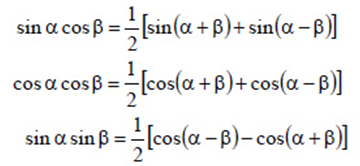
Формулы преобразования суммы тригонометрических функций в произведение

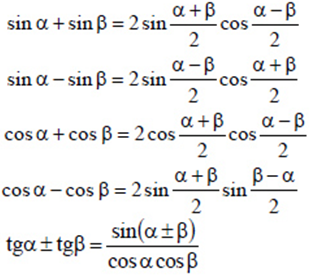
Формулы, выражающие $\sin \alpha ,\ \cos \alpha ,\ \text{tg}\alpha$ через $\text{tg}\frac{\alpha }{2}$

Формулы приведения

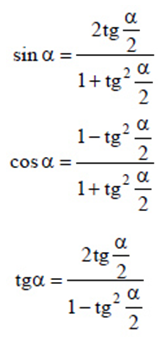
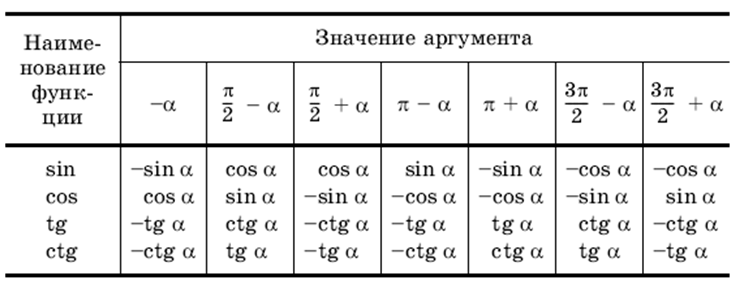
Примеры решения задач

ПРИМЕР 1

Задание

Упростить тригонометрическое выражение

$\text{ctg}\left( -\alpha \right)\cdot \text{tg}\left( -\alpha \right)-{{\sin }^{2}}\left( -\alpha \right)$

Решение

Котангенс, тангенс и синус являются нечетными функциями, поэтому:

$\text{ctg}\left( -\alpha \right)=-\text{ctg}\alpha \text{ };\text{ } \text{tg}\left( -\alpha \right)=-\text{tg}\alpha ; \sin \left( -\alpha \right)=-\sin \alpha$

Этот же результат можно получить используя формулы приведения. Тогда исходное выражение примет вид

$\text{ctg}\left( -\alpha \right)\cdot \text{tg}\left( -\alpha \right)-{{\sin }^{2}}\left( -\alpha \right)=-\text{ctg}\alpha \cdot \left( -\text{tg}\alpha \right)-{{\left( -\sin \alpha \right)}^{2}}=\text{ctg}\alpha \cdot \text{tg}\alpha -{{\sin }^{2}}\alpha$

Учитывая, что $\text{ctg}\alpha \cdot \text{tg}\alpha =1$ , получим

$\text{ctg}\left( -\alpha \right)\cdot \text{tg}\left( -\alpha \right)-{{\sin }^{2}}\left( -\alpha \right)=1-{{\sin }^{2}}\alpha$

Из основного тригонометрического тождества ${{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1$ следует, $1-{{\sin }^{2}}\alpha ={{\cos }^{2}}\alpha$ . Тогда окончательно получим

$\text{ctg}\left( -\alpha \right)\cdot \text{tg}\left( -\alpha \right)-{{\sin }^{2}}\left( -\alpha \right)={{\cos }^{2}}\alpha$

Ответ

$\text{ctg}\left( -\alpha \right)\cdot \text{tg}\left( -\alpha \right)-{{\sin }^{2}}\left( -\alpha \right)={{\cos }^{2}}\alpha$

ПРИМЕР 2

Задание

Упростить тригонометрическое выражение

$\frac{\cos \alpha \cos \beta -\cos \,\left( \alpha +\beta \right)}{\cos \,\left( \alpha -\beta \right)-\sin \alpha \sin \beta }$

Решение

Используя тригонометрические формулы суммы и разности углов, преобразуем в числителе $\cos \,\left( \alpha +\beta \right)=\cos \,\alpha \cos \,\beta -\sin \,\alpha \sin \,\beta$ , а в знаменателе $\cos \,\left( \alpha -\beta \right)=\cos \,\alpha \cos \,\beta +\sin \,\alpha \sin \,\beta$ , получим:

$\frac{\cos \alpha \cos \beta -\cos \,\left( \alpha +\beta \right)}{\cos \,\left( \alpha -\beta \right)-\sin \alpha \sin \beta }=$

$=\frac{\cos \alpha \cos \beta -\left( \cos \,\alpha \cos \,\beta -\sin \,\alpha \sin \,\beta \right)}{\cos \,\alpha \cos \,\beta +\sin \,\alpha \sin \,\beta -\sin \alpha \sin \beta }=$

$=\frac{\cos \alpha \cos \beta -\cos \,\alpha \cos \,\beta +\sin \,\alpha \sin \,\beta }{\cos \,\alpha \cos \,\beta +\sin \,\alpha \sin \,\beta -\sin \alpha \sin \beta }=$

$=\frac{\sin \,\alpha \sin \,\beta }{\cos \,\alpha \cos \,\beta }=\frac{\sin \,\alpha }{\cos \,\alpha }\cdot \frac{\sin \,\beta }{\cos \,\beta }$

По определению $\frac{\sin \,\alpha }{\cos \,\alpha }=\text{tg}\alpha$ , тогда окончательно исходное выражение равно

$\frac{\cos \alpha \cos \beta -\cos \,\left( \alpha +\beta \right)}{\cos \,\left( \alpha -\beta \right)-\sin \alpha \sin \beta }=\text{tg}\alpha \cdot \text{tg}\beta$

Ответ

ПРИМЕР 3

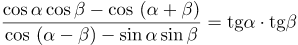Задание

Упростить тригонометрическое выражение

$\sin \left( \pi -2\alpha \right)+2\cos \left( \frac{3}{2}\pi +\alpha \right)\cdot \sin \left( \frac{3}{2}\pi +\alpha \right)$

Решение

Используя формулы тригонометрических функций двойного аргумента, второе слагаемое данного выражение запишется следующим образом

$2\cos \left( \frac{3}{2}\pi +\alpha \right)\cdot \sin \left( \frac{3}{2}\pi +\alpha \right)=\sin \left( 2\cdot \left( \frac{3}{2}\pi +\alpha \right) \right)=\sin \left( 3\pi +2\alpha \right)$

Подставляя это в исходное выражение, получим

$\sin \left( \pi -2\alpha \right)+2\cos \left( \frac{3}{2}\pi +\alpha \right)\cdot \sin \left( \frac{3}{2}\pi +\alpha \right)=\sin \left( \pi -2\alpha \right)+\sin \left( 3\pi +2\alpha \right)$

Далее, учитывая периодичность синуса

$\sin \left( 3\pi +2\alpha \right)=\sin \left( 2\pi +\pi +2\alpha \right)=\sin \left( \pi +2\alpha \right)$

исходное выражение примет вид

$\sin \left( \pi -2\alpha \right)+2\cos \left( \frac{3}{2}\pi +\alpha \right)\cdot \sin \left( \frac{3}{2}\pi +\alpha \right)=\sin \left( \pi -2\alpha \right)+\sin \left( \pi +2\alpha \right)$

Воспользовавшись формулами приведения, окончательно получим:

$\sin \left( \pi -2\alpha \right)+2\cos \,\left( \frac{3}{2}\pi +\alpha \right)\cdot \sin \left( \frac{3}{2}\pi +\alpha \right)=\sin 2\alpha -\sin 2\alpha =0$

Ответ

$\sin \left( \pi -2\alpha \right)+2\cos \,\left( \frac{3}{2}\pi +\alpha \right)\cdot \sin \left( \frac{3}{2}\pi +\alpha \right)=0$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Упрощение тригонометрических выражений

Основные тригонометрические формулы

Примеры решения задач