Тригонометрические тождества

Основные тригонометрические тождества, наиболее часто используемые при выполнении тригонометрических преобразований:

${{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1\qquad(1)$

$\text{tg}\alpha \cdot \text{ctg}\alpha =1\qquad(2)$

$\text{tg}\alpha =\frac{\sin \alpha }{\cos \alpha }\qquad(3)$

$\text{ctg}\alpha =\frac{\cos \alpha }{\sin \alpha }\qquad(4)$

$1+\text{tg}^{2}}\alpha =\frac{1}{{{\cos }^{2}}\alpha }\qquad(5)$

$1+\text{ctg}^{2}}\alpha =\frac{1}{{{\sin }^{2}}\alpha }\qquad(6)$

Примеры решения задач

ПРИМЕР 1

Задание

Доказать тождество ${{\sin }^{6}}\alpha +3{{\sin }^{2}}\alpha {{\cos }^{2}}\alpha +{{\cos }^{6}}\alpha =1$

Доказательство

Из основного тригонометрического тождества (1) выразим синус:

${{\sin }^{2}}\alpha =1-{{\cos }^{2}}\alpha$

Тогда доказываемое тождество представим в виде:

${{\sin }^{6}}\alpha +3{{\sin }^{2}}\alpha {{\cos }^{2}}\alpha +{{\cos }^{6}}\alpha ={{\left( {{\sin }^{2}}\alpha \right)}^{3}}+3{{\sin }^{2}}\alpha {{\cos }^{2}}\alpha +{{\cos }^{6}}\alpha =$

$={{\left( 1-{{\cos }^{2}}\alpha \right)}^{3}}+3(1-{{\cos }^{2}}\alpha ){{\cos }^{2}}\alpha +{{\cos }^{6}}\alpha =1-3{{\cos }^{2}}\alpha +3{{\cos }^{4}}\alpha -{{\cos }^{6}}\alpha +$

$+3{{\cos }^{2}}\alpha -3{{\cos }^{4}}\alpha +{{\cos }^{6}}\alpha =1$

Что и требовалось доказать.

ПРИМЕР 2

Задание

Если $\text{tg}\alpha =\frac{1}{2}$ найти значение выражения

$\frac{5\cos \alpha +6\sin \alpha }{3\sin \alpha -7\cos \alpha }$

Решение

Воспользуемся тригонометрическим тождеством (5) и выразим косинус через тангенс:

${{\cos }^{2}}\alpha =\frac{1}{1+\text{tg}^{2}}\alpha }=\frac{1}{1+\frac{1}{4}}=\frac{4}{5}$

откуда $\cos \alpha =\pm \frac{2}{\sqrt{5}}$ . С помощью равенства (1) выразим синус:

$\sin \alpha =\pm \sqrt{1-{{\cos }^{2}}\alpha }=\pm \sqrt{1-\frac{4}{5}}=\pm \frac{1}{\sqrt{5}}$

Из условия известно, что значение тангенса положительно. Это означает, что угол $\alpha$ лежит в первой или третьей четверти. Следовательно, значения синуса либо оба положительные, либо оба отрицательные. Таким образом,

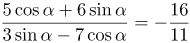$\frac{5\cos \alpha +6\sin \alpha }{3\sin \alpha -7\cos \alpha }=\frac{5\cdot \frac{2}{\sqrt{5}}+6\cdot \frac{1}{\sqrt{5}}}{3\cdot \frac{1}{\sqrt{5}}-7\cdot \frac{2}{\sqrt{5}}}=\frac{\frac{16}{\sqrt{5}}}{\frac{-11}{\sqrt{5}}}=-\frac{16}{11}$

Ответ

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Тригонометрические тождества

Примеры решения задач