Тригонометрические формулы понижения степени

ОПРЕДЕЛЕНИЕ

Формулы понижения степени – это тригонометрические формулы позволяющие перейти от степеней тригонометрических функций к функциям в первой степени, но от кратного аргумента.

Формулы понижения степени для квадрата

Чаще всего на практике используются формулы понижения степени для квадрата:

${{\sin }^{2}}\alpha =\frac{1}{2}\cdot \left( 1-\cos 2\alpha \right); \qquad {{\cos }^{2}}\alpha =\frac{1}{2}\cdot \left( 1+\cos 2\alpha \right)\qquad\qquad(1)$

Формулы (1) напрямую следуют из формул косинуса двойного угла:

$\cos 2\alpha =1-2{{\sin }^{2}}\alpha \quad \Rightarrow \quad 2{{\sin }^{2}}\alpha =1-\cos 2\alpha \quad \Rightarrow \quad {{\sin }^{2}}\alpha =\frac{1-\cos 2\alpha }{2}$

$\cos 2\alpha =2{{\cos }^{2}}\alpha -1\quad \Rightarrow \quad 2{{\cos }^{2}}\alpha =1+\cos 2\alpha \quad \Rightarrow \quad {{\cos }^{2}}\alpha =\frac{1+\cos 2\alpha }{2}$

Формулы понижения степени для куба косинуса или синуса

${{\sin }^{3}}\alpha =\frac{1}{4}\cdot \left( 3\sin \alpha -\sin 3\alpha \right) {{\cos }^{3}}\alpha =\frac{1}{4}\cdot \left( 3\cos \alpha +\cos 3\alpha \right)\qquad\qquad(2)$

Вывести эти формулы можно двумя способами.

Первый способ. Формулы (2) напрямую следуют из тригонометрических функций тройного угла:

$\sin 3\alpha =3\sin \alpha -4{{\sin }^{3}}\alpha \Rightarrow 4{{\sin }^{3}}\alpha =3\sin \alpha -\sin 3\alpha \Rightarrow {{\sin }^{3}}\alpha =\frac{\left( 3\sin \alpha -\sin 3\alpha \right)}{4}$

$\cos 3\alpha =4{{\cos }^{3}}\alpha -3\cos \alpha \Rightarrow 4{{\cos }^{3}}\alpha =3\cos \alpha +\cos 3\alpha \Rightarrow {{\sin }^{3}}\alpha =\frac{\left( 3\cos \alpha +\cos 3\alpha \right)}{4}$

Второй способ. Формулы понижения степени (2) можно вывести, используя формулы (1) и формулы произведения тригонометрических функций. Рассмотрим третью степень синуса

${{\sin }^{3}}\alpha =\sin \alpha \cdot {{\sin }^{2}}\alpha$

Применим одну из формул (1)

${{\sin }^{3}}\alpha =\sin \alpha \cdot {{\sin }^{2}}\alpha =\sin \alpha \cdot \frac{\left( 1-\cos 2\alpha \right)}{2}=\frac{1}{2}\cdot \left( \sin \alpha -\sin \alpha \cos 2\alpha \right)$

далее применим формулу произведения синусов: $\sin \alpha \cos \beta =\frac{\sin \left( \alpha -\beta \right)+\sin \left( \alpha +\beta \right)}{2}$ :

${{\sin }^{3}}\alpha =\frac{1}{2}\cdot \left( \sin \alpha -\sin \alpha \cos 2\alpha \right)=\frac{1}{2}\cdot \left( \sin \alpha -\frac{\sin \left( -\alpha \right)}{2}-\frac{\sin 3\alpha }{2} \right)=$

$=\frac{1}{2}\cdot \left( \sin \alpha +\frac{\sin \alpha }{2}-\frac{\sin 3\alpha }{2} \right)=\frac{1}{2}\cdot \left( \frac{3\sin \alpha }{2}-\frac{\sin 3\alpha }{2} \right)=\frac{1}{4}\left( 3\sin \alpha -\sin 3\alpha \right)$

Аналогично,

${{\cos }^{3}}\alpha =\cos \alpha \cdot {{\cos }^{2}}\alpha =\cos \alpha \cdot \frac{\left( 1+\cos 2\alpha \right)}{2}=\frac{1}{2}\cdot \left( \cos \alpha +\cos \alpha \cos 2\alpha \right)$

далее применим формулу произведения косинусов: $\cos \alpha \cos \beta =\frac{\cos \left( \alpha -\beta \right)+\cos \left( \alpha +\beta \right)}{2}$ :

${{\cos }^{3}}\alpha =\cos \frac{1}{2}\cdot \left( \cos \alpha +\cos \alpha \cos 2\alpha \right)=\frac{1}{2}\cdot \left( \cos \alpha +\frac{\cos \left( -\alpha \right)}{2}+\frac{\cos 3\alpha }{2} \right)=$

$=\frac{1}{2}\cdot \left( \cos \alpha +\frac{\cos \alpha }{2}+\frac{\cos 3\alpha }{2} \right)=\frac{1}{2}\cdot \left( \frac{3\cos \alpha }{2}+\frac{\cos 3\alpha }{2} \right)=\frac{1}{4}\left( 3\cos \alpha +\cos 3\alpha \right)$

Формулы понижения степени для четвертой степени косинуса или синуса

${{\sin }^{4}}\alpha =\frac{1}{8}\cdot \left( \cos 4\alpha -4\cos 2\alpha +3 \right).{{\cos }^{4}}\alpha =\frac{1}{8}\cdot \left( \cos 4\alpha +4\cos 2\alpha +3 \right)$

Эти формулы доказываются применением к ним дважды формул (1):

${{\sin }^{4}}\alpha ={{\left( {{\sin }^{2}}\alpha \right)}^{2}}={{\left( \frac{1-\cos 2\alpha }{2} \right)}^{2}}=\frac{1}{4}\left( 1+2\cos 2\alpha +{{\cos }^{2}}2\alpha \right)=$

$=\frac{1}{4}\left( 1-2\cos 2\alpha +\frac{1+\cos 4\alpha }{2} \right)=\frac{1}{4}\left( \frac{3}{2}-\frac{4\cos 2\alpha }{2}+\frac{\cos 4\alpha }{2} \right)=\frac{1}{8}\left( \cos 4\alpha -4\cos 2\alpha +3 \right)$

${{\cos }^{4}}\alpha ={{\left( {{\cos }^{2}}\alpha \right)}^{2}}={{\left( \frac{1+\cos 2\alpha }{2} \right)}^{2}}=\frac{1}{4}\left( 1+2\cos 2\alpha +{{\cos }^{2}}2\alpha \right)=$

$=\frac{1}{4}\left( 1+2\cos 2\alpha +\frac{1+\cos 4\alpha }{2} \right)=\frac{1}{4}\left( \frac{3}{2}+\frac{4\cos 2\alpha }{2}+\frac{\cos 4\alpha }{2} \right)=\frac{1}{8}\left( \cos 4\alpha +4\cos 2\alpha +3 \right)$

Примеры решения задач

ПРИМЕР 1

Задание

Понизить степень следующих выражений

1) ${{\cos }^{2}}4x$

2) ${{\sin }^{2}}3x$

Решение

1) Воспользуемся формулой понижения степени для квадрата косинуса ${{\cos }^{2}}\alpha =\frac{1}{2}\cdot \left( 1+\cos 2\alpha \right)$ , получим:

${{\cos }^{2}}4x=\frac{1+\cos 2\cdot 4x}{2}=\frac{1+\cos 8x}{2}$

2) Применим формулы понижения степени для синуса ${{\sin }^{2}}\alpha =\frac{1}{2}\cdot \left( 1-\cos 2\alpha \right)$

${{\sin }^{2}}3x=\frac{1-\cos 2\cdot 3x}{2}=\frac{1-\cos 6x}{2}$

Ответ

ПРИМЕР 2

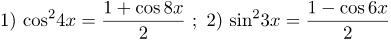Задание

Вычислить, используя формулы понижения степени

$1) \text{ } {{\sin }^{2}}\frac{\pi }{8}$

$2) \text{ } {{\cos }^{2}}\frac{\pi }{12}$

Решение

1) Понизим степень синуса, используя формулу ${{\sin }^{2}}\alpha =\frac{1}{2}\cdot \left( 1-\cos 2\alpha \right)$ , получим

${{\sin }^{2}}\frac{\pi }{8}=\frac{1}{2}\cdot \left( 1-\cos 2\cdot \frac{\pi }{8} \right)=\frac{1}{2}\cdot \left( 1-\cos 2\cdot \frac{\pi }{8} \right)=\frac{1}{2}\cdot \left( 1-\cos \frac{\pi }{4} \right)$

Учитывая, что $\cos \frac{\pi }{4}=\frac{\sqrt{2}}{2}$ , окончательно имеем:

${{\sin }^{2}}\frac{\pi }{8}=\frac{1}{2}\cdot \left( 1-\cos \frac{\pi }{4} \right)=\frac{1}{2}\cdot \left( 1-\frac{\sqrt{2}}{2} \right)=\frac{1}{2}\cdot \left( \frac{2-\sqrt{2}}{2} \right)=\frac{2-\sqrt{2}}{4}$

2) Применим к исходному выражению формулу понижения степени ${{\cos }^{2}}\alpha =\frac{1}{2}\cdot \left( 1+\cos 2\alpha \right)$ , получим:

${{\cos }^{2}}\frac{\pi }{12}=\frac{1}{2}\cdot \left( 1+\cos 2\cdot \frac{\pi }{12} \right)=\frac{1}{2}\cdot \left( 1+\cos \frac{\pi }{6} \right)$

Так как $\cos \frac{\pi }{6}=\frac{\sqrt{3}}{2}$ , то окончательно

${{\cos }^{2}}\frac{\pi }{12}=\frac{1}{2}\cdot \left( 1+\cos \frac{\pi }{6} \right)=\frac{1}{2}\cdot \left( 1+\frac{\sqrt{3}}{2} \right)=\frac{1}{2}\cdot \left( \frac{2+\sqrt{3}}{2} \right)=\frac{2+\sqrt{3}}{4}$

Ответ

ПРИМЕР 3

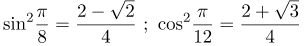Задание

Доказать тождество $2{{\sin }^{2}}\frac{\alpha }{2}+\cos \alpha =1$

Решение

По формуле понижения степени ${{\sin }^{2}}\alpha =\frac{1}{2}\cdot \left( 1-\cos 2\alpha \right)$ :

${{\sin }^{2}}\frac{\alpha }{2}=\frac{1}{2}\left( 1-\cos 2\cdot \frac{\alpha }{2} \right)\quad \Rightarrow \quad {{\sin }^{2}}\frac{\alpha }{2}=\frac{1}{2}\left( 1-\cos \alpha \right)\quad \Rightarrow \quad 2{{\sin }^{2}}\frac{\alpha }{2}=1-\cos \alpha$

Подставим полученное выражение в исходное тождество

$1-\cos \alpha +\cos \alpha =1\quad \Rightarrow \quad 1=1$

Что и требовалось доказать.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Тригонометрические формулы понижения степени

Формулы понижения степени для квадрата

Формулы понижения степени для куба косинуса или синуса

Формулы понижения степени для четвертой степени косинуса или синуса

Примеры решения задач