Тангенс суммы
ОПРЕДЕЛЕНИЕ
Тангенс суммы двух углов вычисляется по формуле
![Rendered by QuickLaTeX.com \[ \text{tg}(\alpha +\beta )=\frac{\text{tg}\alpha +\text{tg}\beta }{1-\text{tg}\alpha \cdot \text{tg}\beta }\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-cded39e0ceedbafeac2cbaf3cdf4e1ef_l3.png)
Примеры решения задач
ПРИМЕР 1
| Задание | Вычислить |
| Решение | Представим угол |
| Ответ |
ПРИМЕР 2
| Задание | Упростить выражение
|
| Решение | Данное выражение является правой частью в формуле для тангенса суммы углов Из таблицы значений тригонометрических функций известно, что |
| Ответ | 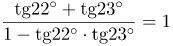 |











