Синус тройного угла
ОПРЕДЕЛЕНИЕ
Синус тройного угла выражается через синус этого угла следующим образом
![]()
Примеры решения задач
ПРИМЕР 1
| Задание | Найти значение |
| Решение | Пользуясь основными тригонометрическими тождествами выразим синус через котангенс
откуда Подставим полученное значение в формулу синуса тройного угла |
| Ответ | 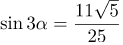 |
ПРИМЕР 2
| Задание | Упростить выражение
|
| Решение | Используя формулу синуса тройного угла, преобразуем выражение
|
| Ответ | 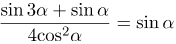 |











