Синус суммы
ОПРЕДЕЛЕНИЕ
Синус суммы двух углов вычисляется по формуле
![]()
Примеры решения задач
ПРИМЕР 1
| Задание | Вычислить |
| Решение | Представим |
| Ответ | 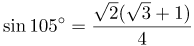 |
ПРИМЕР 2
| Задание | Упростить выражение
|
| Решение | Выражения в числителе и знаменателе преобразуем с помощью формулы синуса суммы:
|
| Ответ | 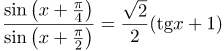 |






![Rendered by QuickLaTeX.com \[ \frac{\sin \left( x+\frac{\pi }{4} \right)}{\sin \left( x+\frac{\pi }{2} \right)} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-82b5c5d88777ca433db2920899df0941_l3.png)
![Rendered by QuickLaTeX.com \[\frac{\sin \left( x+\frac{\pi }{4} \right)}{\sin \left( x+\frac{\pi }{2} \right)}=\frac{\sin x\cos \frac{\pi }{4}+\cos x\sin \frac{\pi }{4}}{\sin x\cos \frac{\pi }{2}+\cos x\sin \frac{\pi }{2}}=\frac{\sin x\cdot \frac{\sqrt{2}}{2}+\cos x\cdot \frac{\sqrt{2}}{2}}{\sin x\cdot 0+\cos x\cdot 1}=\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f6591a8814be4ca5ad6c14ab23cf03ca_l3.png)





