Синус половинного угла
ОПРЕДЕЛЕНИЕ
Синус половинного угла выражается формулой, которая связывает функцию угла 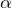 и функцию угла
и функцию угла 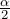 формуле
формуле
![Rendered by QuickLaTeX.com \[ \sin \frac{\alpha }{2}=\pm \sqrt{\frac{1-\cos \alpha }{2}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-31a735338fa77304a9911c0b77bc93c9_l3.png)
Вывод формулы синуса половинного угла
Получить эту формулу можно используя формулу косинуса двойного угла следующим образом:
![]()
откуда
![]()
Эту формулу еще называют формулой понижения степени синуса.
Примеры решения задач
ПРИМЕР 1
| Задание | Вычислить
|
| Решение | Для вычисления данного интеграла воспользуемся формулой половинного угла синуса
|
| Ответ | 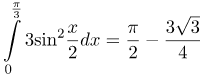 |
ПРИМЕР 2
| Задание | Упростить выражение
|
| Решение | Чтобы упростить данное выражение будем использовать формулу понижения степени синуса, а также представим тангенс в виде |
| Ответ | 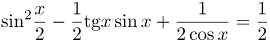 |






![Rendered by QuickLaTeX.com \[ \int\limits_{0}^{\frac{\pi }{3}}{3{{\sin }^{2}}}\frac{x}{2}dx \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b4f3a0cd5a20ee02ab7ad3c8eaa75136_l3.png)
![Rendered by QuickLaTeX.com \[ \int\limits_{0}^{\frac{\pi }{3}}{3{{\sin }^{2}}}\frac{x}{2}dx=3\int\limits_{0}^{\frac{\pi }{3}}{\frac{1-\cos x}{2}}dx=\frac{3}{2}\left( \int\limits_{0}^{\frac{\pi }{3}}{dx-\int\limits_{0}^{\frac{\pi }{3}}{\cos x}}dx \right)=\frac{3}{2}\left( x|_{0}^{\frac{\pi }{3}}-\sin x|_{0}^{\frac{\pi }{3}} \right)=\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-464252d1e6edcb9eca5e8cb978741c20_l3.png)
![Rendered by QuickLaTeX.com \[ =\frac{3}{2}\left( \frac{\pi }{3}-0-\sin \frac{\pi }{3}+\sin 0 \right)=\frac{3}{2}\left( \frac{\pi }{3}-\frac{\sqrt{3}}{2} \right)=\frac{\pi }{2}-\frac{3\sqrt{3}}{4}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-df75eb23c1016c2265507828019153c0_l3.png)





