Разность тангенсов
ОПРЕДЕЛЕНИЕ
Разность тангенсов двух углов 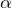 и
и 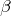 равна отношению синуса разности
равна отношению синуса разности  к произведению косинусов этих углов:
к произведению косинусов этих углов:
![Rendered by QuickLaTeX.com \[ \text{tg}\alpha -\text{tg}\beta =\frac{\sin (\alpha -\beta )}{\cos \alpha \cdot \cos \beta }\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-0fcd1082696eb52148343c62e9e16b18_l3.png)
Примеры решения задач
ПРИМЕР 1
| Задание | Упростить выражение |
| Решение | Воспользуемся формулой разности тангенсов
Так как синус – функция нечетная, то Косинус функция четная, а значит |
| Ответ | 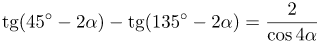 |
ПРИМЕР 2
| Задание | Найти значение выражения |
| Решение | Представим искомую разность в виде
|
| Ответ |






![Rendered by QuickLaTeX.com \[\text{tg}\frac{11\pi }{12}-\text{tg}\frac{5\pi }{12}=\frac{\sin \left( \frac{11\pi }{12}-\frac{5\pi }{12} \right)}{\cos \frac{11\pi }{12}\cdot \cos \frac{5\pi }{12}}=\frac{\sin \frac{\pi }{2}}{\frac{1}{2}\left( \cos \frac{\pi }{2}+\cos \frac{4\pi }{3} \right)}=\frac{2}{\cos \left( \pi +\frac{\pi }{3} \right)}=\frac{2}{-\frac{1}{2}}=-4\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2fac9486f40d3d5a9bbf641b0f2e55d2_l3.png)





