Котангенс угла
Определение и формула котангенса
Котангенс угла ![]() обозначается
обозначается ![]() .
.
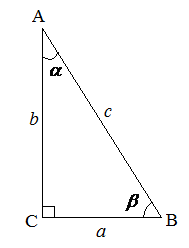
Рис.1
Рассмотрим прямоугольный треугольник ![]() с
с ![]() , гипотенузой
, гипотенузой ![]() и катетами
и катетами ![]() и
и ![]() (рис.1). Тогда
(рис.1). Тогда
![]()
Рассмотрим окружность радиуса 1 с центром в начале координат. Выберем произвольный угол ![]() , которому на окружности соответствует точка
, которому на окружности соответствует точка ![]() .
.
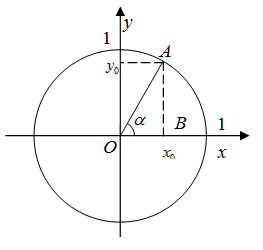
Опустим перпендикуляры на оси координат, тогда
![]()
т.е. котангенсом угла есть отношение абсциссы точки А к ее ординате. Так как синус угла равен значению ординаты точки А, а косинус угла равен значению абсциссы, то
![]()
Функция ![]() является периодической с периодом
является периодической с периодом ![]() , т.е.
, т.е.
![]()
Примеры решения задач
| Задание | В прямоугольном треугольнике 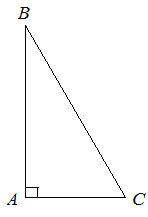
|
| Решение | Так как котангенс острого угла в прямоугольном треугольнике равен отношению прилежащего катета к противолежащему, то можем записать, что
|
| Ответ |
| Задание | Найти |
| Решение | Преобразуем заданное выражение следующим образом:
или Так как |
| Ответ |











