Косинус в квадрате
![]()
Эта формула называется формулой понижения степени косинуса.
Примеры решения задач
| Задание | Вычислить интеграл
|
| Решение | Для того чтобы упростить подынтегральную функцию, будем использовать формулу понижения степени косинуса:
|
| Ответ | 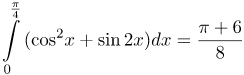 |
| Задание | Упростить выражение
|
| Решение | Упростим выражение с помощью формулы квадрата косинуса:
Преобразуем каждый из членов разности следующим образом: и Тогда Полученное выражение представляет собой правую часть формулы произведения синусов, т.е. |
| Ответ | 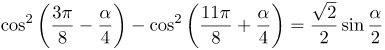 |






![Rendered by QuickLaTeX.com \[ \int\limits_{0}^{\frac{\pi }{4}}{({{\cos }^{2}}}x+\sin 2x)dx \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9185553952c7fb23d1a677480dbff637_l3.png)
![Rendered by QuickLaTeX.com \[ \int\limits_{0}^{\frac{\pi }{4}}{({{\cos }^{2}}}x+\sin 2x)dx=\int\limits_{0}^{\frac{\pi }{4}}{\left( \frac{1+\cos 2x}{2}+\sin 2x \right)}dx= \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-079c7c44b107b4dccbd43b511a5aac6a_l3.png)
![Rendered by QuickLaTeX.com \[ =\frac{1}{2}\left( \int\limits_{0}^{\frac{\pi }{4}}{dx}+\int\limits_{0}^{\frac{\pi }{4}}{\cos 2xdx} \right)+\int\limits_{0}^{\frac{\pi }{4}}{\sin 2x}dx=\frac{1}{2}\left. \left( x+\frac{\sin 2x}{2} \right) \right|_{0}^{\frac{\pi }{4}}-\left. \frac{\cos 2x}{2} \right|_{0}^{\frac{\pi }{4}}= \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-59e763cd1e2e2acc637413733744a57a_l3.png)





