Косинус разности
Косинус разности двух углов равен сумме произведения косинусов и произведения синусов данных углов:
![]()
Примеры решения задач
ПРИМЕР 1
| Задание | Преобразовать выражение |
| Решение | Преобразуем исходное выражение, используя формулу косинуса разности Учитывая, что |
| Ответ |
ПРИМЕР 2
| Задание | Преобразовать выражение |
| Решение | Воспользуемся формулой косинуса разности углов, получим
Учитывая, что |
| Ответ | 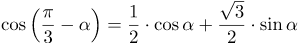 |











