Косинус половинного угла
ОПРЕДЕЛЕНИЕ
Косинус половинного угла выражается формулой, которая связывает функцию угла 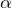 и функцию угла
и функцию угла 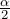 формуле
формуле
![Rendered by QuickLaTeX.com \[ \cos \frac{\alpha }{2}=\pm \sqrt{\frac{1+\cos \alpha }{2}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-909a15ca9b17cc8f90e2795ada2f592e_l3.png)
Вывод формулы косинуса половинного угла
Получить эту формулу можно используя формулу косинуса двойного угла следующим образом:
![]()
откуда
![]()
Эту формулу еще называют формулой понижения степени косинуса.
Примеры решения задач
ПРИМЕР 1
| Задание | Найти значение выражения |
| Решение | Используя формулу половинного угла косинуса, упростим данное выражение и подставим известное значение косинуса
|
| Ответ | 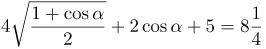 |
ПРИМЕР 2
| Задание | Упростить выражение
|
| Решение | Упростим выражение с помощью формулы понижения степени косинуса:
а Следовательно, |
| Ответ | 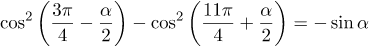 |






![Rendered by QuickLaTeX.com \[4\sqrt{\frac{1+\cos \alpha }{2}}+2\cos \alpha +5=4\sqrt{\frac{1+\frac{1}{8}}{2}}+2\cdot \frac{1}{8}+5=4\sqrt{\frac{9}{16}}+\frac{1}{4}+5=8\frac{1}{4}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ee8de58fc78c46946094be407f18ca71_l3.png)





