Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Тригонометрия Гиперболический тангенс

Гиперболический тангенс

ОПРЕДЕЛЕНИЕ

Гиперболическим тангенсом называется функция вида

$\text{th}x=\frac{\text{sh}x}{\text{ch}x}$

или через экспоненту

$\text{th}x=\frac{{{e}^{x}}-{{e}^{-x}}}{{{e}^{x}}+{{e}^{-x}}}=\frac{{{e}^{2x}}-1}{{{e}^{2x}}+1}$

причем $-\infty <x<+\infty ,\quad -1<y<1$ .

Свойства гиперболического тангенса

Тангенс гиперболический является возрастающей нечетной функцией, т.е.

$\text{th}(-x)=-\text{th}x$

График функции $y=\text{th}x$ изображен на рисунке 1.

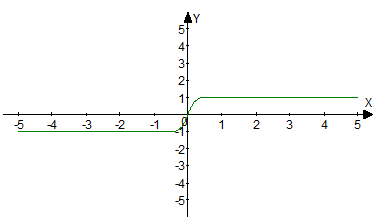
Рис. 1

Связь между гиперболическим и круговым тангенсами

$\text{th}x=-i\cdot \text{tg}(ix),$

$\text{th}(ix)=-i\cdot \text{tg}x$

где $i$ – мнимая единица.

Формула сложения

$\text{th}(x\pm y)=\frac{\text{th}x\pm \text{th}y}{1\pm \text{th}x\cdot \text{th}y}$

Формула двойного угла

$\text{th}2x=\frac{2\text{th}x}{1+\text{th}^{2}}x}$

Произведение тангенсов гиперболических

$\text{th}x\cdot \text{th}y=\frac{\text{ch}(x+y)-\text{ch}(x-y)}{\text{ch}(x+y)+\text{ch}(x-y)}$

Формула суммы (разности) тангенсов гиперболических

$\text{th}x\pm \text{th}y=\frac{\text{sh}(x\pm y)}{\text{ch}x\cdot \text{ch}y}$

Производная тангенса гиперболического

$(\text{th}x{)}'=\frac{1}{\text{ch}^{2}}x}$

Интеграл

$\int{\text{th}x}dx=\ln \text{ch}x+C$

Примеры решения задач

ПРИМЕР 1

Задание

Вычислить интеграл

$\int{({{e}^{x}}+{{e}^{-x}})\cdot \text{th}x\text{ }}dx$

Решение

Представим тангенс гиперболический в виде

$\text{th}x=\frac{{{e}^{x}}-{{e}^{-x}}}{{{e}^{x}}+{{e}^{-x}}}$

и подставим в интеграл:

$\int{({{e}^{x}}+{{e}^{-x}})\cdot \frac{{{e}^{x}}-{{e}^{-x}}}{{{e}^{x}}+{{e}^{-x}}}}dx=\int{({{e}^{x}}-{{e}^{-x}})}dx=\int{{{e}^{x}}}dx-\int{{{e}^{-x}}}dx=$

$={{e}^{x}}-(-{{e}^{-x}})+C={{e}^{x}}+{{e}^{-x}}+C$

Ответ

$\int{({{e}^{x}}+{{e}^{-x}})\cdot \text{th}x\text{ }}dx={{e}^{x}}+{{e}^{-x}}+C$

ПРИМЕР 2

Задание

Найти приближенное значение $\text{th}\ 2$

Решение

Пользуясь определением тангенса гиперболического

$\text{th}x=\frac{{{e}^{2x}}-1}{{{e}^{2x}}+1}$

, можно записать, что

$\text{th}2=\frac{{{e}^{2\cdot 2}}-1}{{{e}^{2\cdot 2}}+1}=\frac{{{\left( 2,72 \right)}^{4}}-1}{{{\left( 2,72 \right)}^{4}}+1}=\frac{54,7363-1}{54,7363+1}=\frac{53,7363}{55,7363}=0,9641$

Ответ

$\text{th}\ 2=0,9641$

Читайте также:

Котангенс угла

Котангенс двойного угла

Котангенс половинного угла

График котангенса

Сумма котангенсов

Разность котангенсов

Котангенс суммы

Сумма тангенсов

© SolverBook - онлайн сервисы для учебы, 2015

Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Почта для связи: info@ru.solverbook.com

Выберите язык:

Сервисы

SolverBook