Формулы тангенсов

ОПРЕДЕЛЕНИЕ

Тангенсом угла $\alpha$ называется отношения синуса угла к косинусу этого же угла. Тангенс угла $\alpha$ обозначается $\text{tg}\alpha$ . Тогда

$\text{tg}\alpha =\frac{\sin \alpha }{\cos \alpha }$

Тангенс половинного угла

$\text{tg}\frac{\alpha }{2}=\frac{1-\cos \alpha }{\sin \alpha }=\frac{\sin \alpha }{1+\cos \alpha }$

Также тангенс половинного угла выражается в виде

$\text{tg}\frac{\alpha }{2}=\sqrt{\frac{1-\cos \alpha }{1+\cos \alpha }}$

Через тангенс половинного угла можно выразить все тригонометрические функции:

$\sin \alpha =\frac{2\text{tg}\frac{\alpha }{2}}{1+\text{tg}^{2}\frac{\alpha }{2}}, \quad \cos \alpha =\frac{1-\text{tg}^{2}\frac{\alpha }{2}}{1+\text{tg}^{2}\frac{\alpha }{2}}, \quad \text{tg}\alpha =\frac{2\text{tg}\frac{\alpha }{2}}{1-\text{tg}^{2}\frac{\alpha }{2}}, \quad \text{tg}\alpha =\frac{1-\text{tg}^{2}\frac{\alpha }{2}}{2\text{tg}\frac{\alpha }{2}}$

Тангенс двойного угла

$\text{tg}2\alpha =\frac{2\text{tg}\alpha }{1-\text{tg}^{2}\alpha }$

Тангенс тройного угла

$\text{tg}3\alpha =\frac{3\text{tg}\alpha -\text{tg}^{3}\alpha }{1-3\text{tg}^{2}\alpha}$

Сумма тангенсов

$\text{tg}\alpha +\text{tg}\beta =\frac{\sin (\alpha +\beta )}{\cos \alpha \cdot \cos \beta }$

Разность тангенсов

$\text{tg}\alpha -\text{tg}\beta =\frac{\sin (\alpha -\beta )}{\cos \alpha \cdot \cos \beta }$

Тангенс суммы двух углов

$\text{tg}(\alpha +\beta )=\frac{\text{tg}\alpha +\text{tg}\beta }{1-\text{tg}\alpha \cdot \text{tg}\beta }$

Тангенс разности двух углов

$\text{tg}(\alpha -\beta )=\frac{\text{tg}\alpha -\text{tg}\beta }{1+\text{tg}\alpha \cdot \text{tg}\beta }$

Квадрат тангенса

$\text{tg}^{2}\alpha =\frac{1-\cos 2\alpha }{1+\cos 2\alpha }$

ТЕОРЕМА

Теорема тангенсов. Разность двух сторон треугольника относится к их сумме, как тангенс полуразности противолежащих углов к тангенсу полусуммы этих углов:

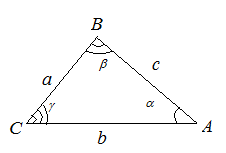
$\frac{a-b}{a+b}=\frac{\text{tg}\frac{\alpha -\beta }{2}}{\text{tg}\frac{\alpha +\beta }{2}}$

Примеры решения задач

ПРИМЕР 1

Задание

Дано $\text{tg}\frac{\alpha }{2}=\frac{6}{5}$ . Найти $\sin \alpha ,\quad \cos \alpha ,\quad \text{tg}\alpha ,\quad \text{ctg}\alpha$

Решение

Воспользуемся формулами для выражения тригонометрических функций через тангенс половинного угла:

$\sin \alpha =\frac{2\text{tg}\frac{\alpha }{2}}{1+\text{tg}^{2}\frac{\alpha }{2}}=\frac{2\cdot \frac{6}{5}}{1+{{\left( \frac{6}{5} \right)}^{2}}}=\frac{60}{61}, \quad \cos \alpha =\frac{1-\text{tg}^{2}\frac{\alpha }{2}}{1+\text{tg}^{2}\frac{\alpha }{2}}=\frac{1-{{\left( \frac{6}{5} \right)}^{2}}}{1+{{\left( \frac{6}{5} \right)}^{2}}}=-\frac{11}{61}$

$\text{tg}\alpha =\frac{2\text{tg}\frac{\alpha }{2}}{1-\text{tg}^{2}\frac{\alpha }{2}}=\frac{2\cdot \frac{6}{5}}{1-{{\left( \frac{6}{5} \right)}^{2}}}=-\frac{60}{11}, \quad \text{ctg}\alpha =\frac{1-\text{tg}^{2}\frac{\alpha }{2}}{2\text{tg}\frac{\alpha }{2}}=\frac{1-{{\left( \frac{6}{5} \right)}^{2}}}{2\cdot \frac{6}{5}}=-\frac{11}{60}$

Ответ

$\sin \alpha =\frac{60}{61}, \quad \cos \alpha =-\frac{11}{61}, \quad \text{tg}\alpha =-\frac{60}{11}, \quad \text{ctg}\alpha =-\frac{11}{60}$

ПРИМЕР 2

Задание

Доказать тождество

$\text{tg}30^{\circ }+\text{tg}40^{\circ }+\text{tg}50^{\circ }+\text{tg}60^{\circ }=\frac{8\sqrt{3}\cos 20^{\circ }}{3}$

Доказательство

Левую часть тождества перегруппируем и применим формулу суммы тангенсов

$\text{tg}30^{\circ}+\text{tg}40^{\circ}+\text{tg}50^{\circ}+\text{tg}60^{\circ}=(\text{tg}{{30}^{\circ }}+\text{tg}60^{\circ})+(\text{tg}40^{\circ}+\text{tg}50^{\circ})=$

$=\frac{\sin (30^{\circ}+60^{\circ})}{\cos 30^{\circ}\cdot \cos 60^{\circ}}+\frac{\sin (40^{\circ}+50^{\circ})}{\cos 40^{\circ}\cdot \cos 50^{\circ}}=\frac{1}{\cos 30^{\circ}\cdot \cos 60^{\circ}}+\frac{1}{\cos 40^{\circ}\cdot \cos 50^{\circ}}$

К выражениям в знаменателях применим формулу произведения косинусов:

$\frac{1}{\cos 30^{\circ}\cdot \cos 60^{\circ}}+\frac{1}{\cos 40^{\circ}\cdot \cos 50^{\circ}}=\frac{1}{\frac{1}{2}(\cos (30^{\circ}-60^{\circ})+\cos (30^{\circ}+60^{\circ}))}+$

$+\frac{1}{\frac{1}{2}(\cos (40^{\circ}-50^{\circ})+\cos (40^{\circ}+50^{\circ}))}=\frac{2}{\cos 30^{\circ}}+\frac{2}{\cos 10^{\circ}}=\frac{2(\cos 10^{\circ}+\cos 30^{\circ})}{\cos 10^{\circ}\cos 30^{\circ}}=$

$=\frac{4\cos 20^{\circ}\cos 10^{\circ}}{\cos 10^{\circ}\cos 30^{\circ}}=\frac{8\cos 20^{\circ}}{\sqrt{3}}=\frac{8\sqrt{3}\cos 20^{\circ}}{3}$

Что и требовалось доказать.

Понравился сайт? Расскажи друзьям!