Теорема о двух милиционерах
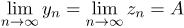 , то и
, то и 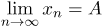
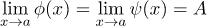 , то существует предел функции и
, то существует предел функции и ![]()
Доказательство теоремы
По определению последовательности, для произвольного числа ![]() , найдется такой номер
, найдется такой номер ![]() , что при
, что при ![]()
![]()
И найдется такой номер ![]() , что при
, что при ![]()
![]()
Рассмотрим так же номер ![]() больший, чем числа
больший, чем числа ![]() и
и ![]() . Тогда при
. Тогда при ![]() выполняются оба предшествующих двойных неравенства, и поэтому
выполняются оба предшествующих двойных неравенства, и поэтому
![]()
![]() или
или ![]()
Следовательно, 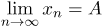
Теорема доказана.
Примеры решения задач
| Задание | Найти предел последовательности |
| Решение | Рассмотрим последовательности Найдем пределы введенных последовательностей. Для последовательности а для последовательности Таким образом, |
| Ответ | 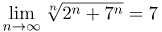 |
| Задание | Найти предел
|
| Решение | Функция Разделим каждую часть неравенства на Вычислим пределы левой и правой частей данного неравенства. Старшие степени числителя и знаменателя совпадают, поэтому предел равен отношению коэффициентам при старших степенях: Оба предела равны друг другу, следовательно, по теореме о двух милиционерах и искомый предел |
| Ответ | 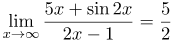 |






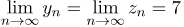 , следовательно, по теореме о двух милиционерах,
, следовательно, по теореме о двух милиционерах,




