Свойства векторов
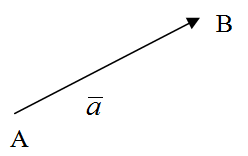
Если концы вектора заданы своими координатами в пространстве ![]() , то координаты вектора
, то координаты вектора
![]()
![]()
Вектор называется единичным, если его длина равна единице. Вектор называется нулевым, если его длина равна нулю.
Векторы ![]() и
и ![]() называются коллинеарными, если они или лежат на одной прямой или на параллельных прямых.
называются коллинеарными, если они или лежат на одной прямой или на параллельных прямых.
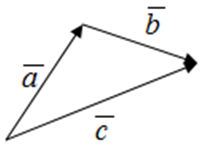
Операция сложения векторов обладает такими свойствами
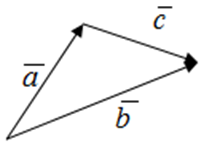
Если векторы ![]() и
и ![]() заданы своими координатами, то сумма/разность этих векторов
заданы своими координатами, то сумма/разность этих векторов
![]()
![]()
Также скалярное произведение векторов можно вычислить как произведение модулей векторов на косинус угла между ними:
![]()
Свойства скалярного произведения
Векторным произведением векторов ![]() и
и ![]() называется вектор
называется вектор ![]() (или
(или ![]() ) такой, что:
) такой, что:
1) вектор ![]() ортогонален векторам
ортогонален векторам ![]() и
и ![]() :
:
![]()
2) векторы ![]() и
и ![]() образуют правую тройку;
образуют правую тройку;
3) модуль векторного произведения равен площади параллелограмма построенного на векторах ![]() и
и ![]() :
:
![]()
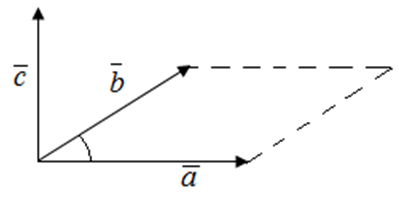
Если векторы ![]() и
и ![]() заданы своими координатами, то векторное произведение находится по формуле:
заданы своими координатами, то векторное произведение находится по формуле:
![Rendered by QuickLaTeX.com \[[\bar{a},\bar{b}]=\left| \begin{matrix} \bar{i} & \bar{j} & \bar{k} \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \\ \end{matrix} \right|\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-90f68463f2dc80338eac8202d525ab8a_l3.png)
Свойства векторного произведения
![Rendered by QuickLaTeX.com [\bar{a},\bar{b}]=-[\bar{b},\bar{a}]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9e2a1c25d669d2ea7e5ed14e5c4d3ac8_l3.png)
![Rendered by QuickLaTeX.com [\bar{a},\bar{b}+\bar{c}]=[\bar{a},\bar{b}]+[\bar{a},\bar{c}]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-a21ba4c4d9403c4c29e8579d172cdadf_l3.png)
![Rendered by QuickLaTeX.com [\lambda \bar{a},\bar{b}]=[\bar{a},\lambda \bar{b}]=\lambda [\bar{a},\bar{b}]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-31f881c2c3621233d49d209d6390c7d1_l3.png)
![Rendered by QuickLaTeX.com [\bar{a},\bar{b}]=\bar{0}](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-04e5d2696f46e38cf06277576aed022f_l3.png) , если векторы
, если векторы 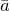 и
и 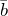 коллинеарные
коллинеарные
![]()
Свойства смешанного произведения
- Смешанное произведение равно нулю, если векторы
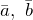 и
и 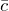 – компланарны
– компланарны - Модуль смешанного произведения трех некомпланарных векторов
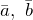 и
и 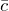 равен объему параллелепипеда, построенного на этих векторах
равен объему параллелепипеда, построенного на этих векторах - Смешанное произведение векторов
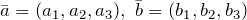 и
и 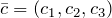 , заданных своими координатами, равно значению определителя, составленного из координат этих векторов:
, заданных своими координатами, равно значению определителя, составленного из координат этих векторов:
![Rendered by QuickLaTeX.com \[(\bar{a},\bar{b},\bar{c})=\left| \begin{matrix} a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \\ c_{1} & c_{2} & c_{3} \\ \end{matrix} \right|\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b5f75a62f641356bfb62b02979e9df44_l3.png)
- Если тройка векторов
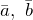 и
и 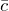 правая, то смешанное произведение
правая, то смешанное произведение 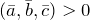 , если левая, то
, если левая, то 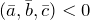
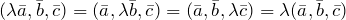
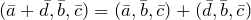
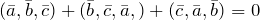
Примеры решения задач
| Задание | Для векторов |
| Решение | Найдем векторы
Найдем разность: |
| Ответ |
| Задание | Найти скалярное и векторное произведение векторов |
| Решение | Скалярное произведение векторов равно сумме произведений соответствующих координат:
Векторное произведение векторов, заданных своими координатами равно т.е. |
| Ответ |






![Rendered by QuickLaTeX.com \[[\bar{a},\bar{b}]=\left| \begin{matrix} \bar{i} & \bar{j} & \bar{k} \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \\ \end{matrix} \right|=\left| \begin{matrix} \bar{i} & \bar{j} & \bar{k} \\ 1 & -3 & 5 \\ 1 & 2 & 0 \\ \end{matrix} \right|=-10\bar{i}+5\bar{j}+5\bar{k}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1b746e268ea2055139546c0f572f0397_l3.png)





