Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Свойства Свойства параллелограмма

Свойства параллелограмма

ОПРЕДЕЛЕНИЕ

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

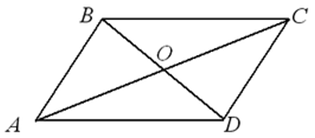
Свойства параллелограмма

Противоположные стороны параллелограмма равны:
$AB=CD; \quad BC=AD$
Противоположные углы параллелограмма равны:
$\angle A=\angle C; \quad \angle B=\angle D$
Точка пересечения диагоналей делит их пополам:
$AO=OC; \quad BO=OD$
Диагональ делит параллелограмм на два равных треугольника $\Delta ABC=\Delta ADC$ .
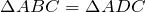Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон:
$A{{C}^{2}}+B{{D}^{2}}=2(A{{B}^{2}}+B{{C}^{2}})$
Сумма углов, прилежащих к одной стороне параллелограмма, равна ${{180}^{\circ}}$ .

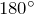Примеры решения задач

ПРИМЕР 1

Задание

В параллелограмме $ABCD$ стороны $AB=3 \ cm$ , а $\angle A={{60}^{\circ}}$ . Найти $\angle B$ и $D$ .

Решение

Углы $\angle A$ и $\angle B$ прилегают к одной стороне, значит $\angle A+\angle B={{180}^{\circ}}$ . Из этого следует, что

$\angle B={{180}^{\circ}}-\angle A={{120}^{\circ}}$

Стороны $AB$ и $CD$ противоположные, значит, они равны, т.е.

$CD=AB=3 \ cm$

Ответ

$\angle B={{120}^{\circ}}$ , $CD=3$ см

ПРИМЕР 2

Задание

В параллелограмме $ABCD$ известны стороны $AB=2 \ cm$ , $BC=4 \ cm$ и диагональ $AC=2\sqrt{3} \ cm$ . Найти вторую диагональ $BD$ .

Решение

Для параллелограмма выполняется следующее равенство:

$A{{C}^{2}}+B{{D}^{2}}=2(A{{B}^{2}}+B{{C}^{2}})$

Подставим в него известные значения $12+B{{D}^{2}}=2(4+16)$ . Выразим

$B{{D}^{2}}=40-12=28$

Следовательно

$BD=2\sqrt{7} \ cm$

Ответ

$BD=2\sqrt{7}$ см

Читайте также:

Свойства диагоналей параллелограмма

Свойства биссектрисы параллелограмма

Свойства квадрата

Свойства диагоналей ромба

Свойства прямоугольника

Свойства диагоналей прямоугольника

© SolverBook - онлайн сервисы для учебы, 2015

Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Почта для связи: info@ru.solverbook.com

Выберите язык:

Сервисы

SolverBook