Свойства касательной, секущей и хорды
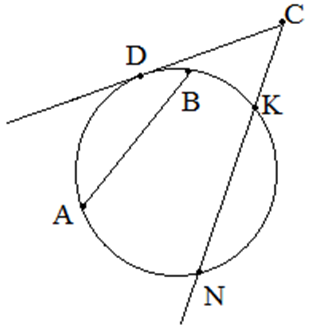
Отрезок, соединяющий две точки окружности, называется хордой (на рисунке это отрезок ![]() ). Хорда, проходящая через центр окружности, называется диаметром окружности.
). Хорда, проходящая через центр окружности, называется диаметром окружности.
Хорда окружности обладает следующими свойствами
- Хорды, находящиеся на одинаковом расстоянии от центра окружности, равны.
- Если хорды стягивают равные центральные углы, то они равны.
- Если диаметр перпендикулярен хорде, то он проходит через ее середину.
- Если вписанные углы опираются на одну хорду, то они равны.
- Две дуги равны, если они заключены между двумя равными хордами.
- Если пара вписанных углов опирается на одну и ту же хорду, а их вершины лежат по разные стороны хорды, то их сумма составляет 180°.
- Для любых двух хорд
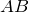 и
и 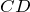 , пересекающихся в точке О, выполняется равенство:
, пересекающихся в точке О, выполняется равенство: 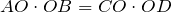 .
.
Прямая, имеющая с окружностью одну общую точку, называется касательной (на рисунке отрезок ![]() ).
).
Прямая, имеющая с окружностью две общие точки, называется секущей (отрезок ![]() ).
).
Свойства касательной и секущей
- Касательная перпендикулярна радиусу, проведенному в точку касания.
- Отрезки касательных, проведенных из одной точки, равны.
- Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть:
![Rendered by QuickLaTeX.com \[AB^{2}=AD\cdot AC\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-39b788809acc97f87a39ea083a237b41_l3.png)
Примеры решения задач
| Задание | В окружности, радиус которой равен 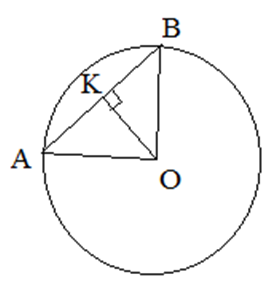
|
| Решение | Концы хорды |
| Ответ |
| Задание | Из точки к окружности проведена касательная 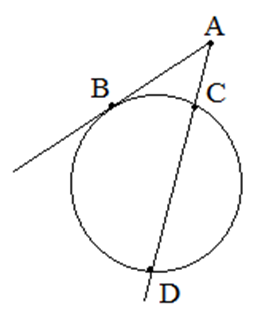
|
| Решение | Из свойств секущей и касательной известно, что Следовательно, откуда |
| Ответ |











