Уравнение прямой

Прямая является одним из фундаментальных понятий геометрии.

Свойства прямой в евклидовой геометрии

1) через любую точку можно провести бесконечно много прямых;

2) через любые две несовпадающие точки можно провести единственную прямую;

3) две несовпадающие прямые на плоскости либо пересекаются в единственной точке, либо являются параллельными;

4) в трёхмерном пространстве существуют три варианта взаимного расположения двух прямых: прямые пересекаются; прямые параллельны; прямые скрещиваются.

Общее уравнение прямой

$Ax+By+C=0 \ (1)$

Здесь $A,\; B$ и $C$ — произвольные постоянные, причём коэффициенты $A$ и $B$ не равны нулю одновременно.

Например. $3x-y+6=0$ .

Частные случаи расположения прямой

Если коэффициент 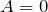$A=0$ , то прямая параллельна оси абсцисс.
Например. $2y+1=0$ .
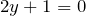В случае, когда постоянная 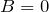$B=0$ , то прямая параллельна оси ординат.
Например. $x+3=0$ .
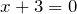Если 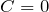$C=0$ , то прямая проходит через начало координат $O\left(0;\; 0\right)$ .
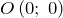Например. $x+y=0$ .

ОПРЕДЕЛЕНИЕ

Нормальным вектором $\bar{n}$ прямой называется вектор, который ей перпендикулярен.

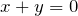Для прямой (1), заданной общим уравнением, нормальный вектор имеет координаты

$\bar{n}=\left(A;\; B\right) \ (2)$

Уравнение прямой по точке и нормальному вектору

Если известно, что прямая проходит через точку $M\left(x_{0} ;\; y_{0} \right)$ и имеет нормальный вектор (2), то ее уравнение имеет вид:

$A\left(x-x_{0} \right)+B\left(y-y_{0} \right)=0$

ПРИМЕР 1

Задание

Записать уравнение прямой, проходящей через точку $M\left(-1;\; 2\right)$ , с нормальным вектором $\bar{n}=\left(1;\; 1\right)$ .

Решение

Согласно формуле, имеем, что искомое уравнение

$1\cdot \left(x-\left(-1\right)\right)+1\cdot \left(y-2\right)=0$

или

$x+1+y-2=0\Rightarrow x+y-1=0$

Ответ

$x+y-1=0$

Уравнение прямой с угловым коэффициентом

ОПРЕДЕЛЕНИЕ

Уравнение прямой, пересекающей ось $Oy$ в точке $\left(0;\; b\right)$ и образующей угол $\varphi$ с положительным направлением оси абсцисс, имеет вид:

$y=kx+b \ (3)$

где $k={\rm tg}\, \varphi$ называется угловым коэффициентом прямой.

ЗАМЕЧАНИЕ

Для прямой (1) угловой коэффициент

$k=-\frac{A}{B}$

Если известно, что прямая проходит через точку $M\left(x_{0} ;\; y_{0} \right)$ и ее угловой коэффициент равен $k$ , то ее уравнение имеет вид:

$y-y_{0} =k\left(x-x_{0} \right)$

ЗАМЕЧАНИЕ

В виде (3) невозможно представить прямую, параллельную оси ординат. Иногда в таком случае формально считают, что угловой коэффициент такой прямой равен бесконечности.

Уравнение прямой в отрезках на осях

Если прямая пересекает ось $Ox$ в точке $\left(a;\; 0\right)$ , а ось ординат — в точке $\left(0;\; b\right)$ , то ее уравнение

$\frac{x}{a} +\frac{y}{b} =1$

ЗАМЕЧАНИЕ

В этом виде невозможно представить прямую, проходящую через начало координат.

ПРИМЕР 2

Задание

Прямая задана общим уравнением $3x-2y-6=0$ . Привести его к уравнению в отрезках на осях.

Решение

Перенесем вначале свободный коэффициент в правую часть равенства:

$3x-2y-6=0\Rightarrow 3x-2y=6$

Делим левую и правую части последнего равенства на 6:

$\left. 3x-2y=6\right|:6\Rightarrow \frac{3x}{6} -\frac{2y}{6} =1\Rightarrow \frac{x}{2} -\frac{y}{3} =1$

Ответ

$\frac{x}{2} -\frac{y}{3} =1$

Нормальное уравнение прямой

$x\cos \alpha +y\sin \alpha -p=0,$

где $p$ — длина перпендикуляра, опущенного на прямую из начала координат, $\alpha$ — угол между положительным направлением оси $Ox$ и направлением этого перпендикуляра.

Если $p=0$ , то прямая проходит через начало координат.

Уравнение прямой, проходящей через две заданные несовпадающие точки

Если прямая проходит через две точки $\left(x_{1} ;\; y_{1} \right)$ и $\left(x_{2} ;\; y_{2} \right)$ , то она задается уравнением

$\frac{x-x_{1} }{x_{2} -x_{1} } =\frac{y-y_{1} }{y_{2} -y_{1} } \ (4)$

или

$\left|\begin{array}{ccc} {x} & {y} & {1} \\ {x_{1} } & {y_{1} } & {1} \\ {x_{2} } & {y_{2} } & {1} \end{array}\right|=0$

Уравнение (4) называется еще каноническим уравнением прямой.

Уравнение прямой по точке и направляющему вектору

Вектор $\bar{l}$ , параллельный прямой, называется направляющим вектором этой прямой.

Если прямая проходит через точку $M\left(x_{0} ;\; y_{0} \right)$ в направлении вектора $\bar{l}=\left(m;\; n\right)$ , то ее уравнение

$\frac{x-x_{0} }{m} =\frac{y-y_{0} }{n}$

Параметрические уравнения прямой

$\left\{\begin{array}{l} {x=mt+x_{0} ,} \\ {y=nt+y_{0} .} \end{array}\right$

Здесь $m,\; n$ — координаты направляющего вектора $\bar{l}$ , $x_{0} ,\; y_{0}$ — координаты точки (абсцисса и ордината соответственно), через которую проходит прямая, $t$ — параметр.

ПРИМЕР 3

Задание

Известно, что прямая проходит через точки $A\left(0;\; -1\right)$ и $B\left(1;\; -2\right)$ . Записать ее параметрические уравнения.

Решение

Вначале запишем уравнение прямой (4), проходящей через две заданные точки:

$\frac{x-0}{1-0} =\frac{y-\left(-1\right)}{-2-\left(-1\right)} \Rightarrow \frac{x}{1} =\frac{y+1}{-1}$

Приравниванием последние отношения к $t$ :

$\frac{x}{1} =\frac{y+1}{-1} =t\Rightarrow \left\{\begin{array}{l} {\frac{x}{1} =t,} \\ {\frac{y+1}{-1} =t} \end{array}\right. \Rightarrow \left\{\begin{array}{l} {x=t,} \\ {y+1=-t} \end{array}\right. \Rightarrow \left\{\begin{array}{l} {x=t,} \\ {y=-t-1.} \end{array}\right.$

Ответ

$\left\{\begin{array}{l} {x=t,} \\ {y=-t-1} \end{array}\right$

Уравнение прямой в полярных координатах

$\rho \left(A\cos \varphi +B\sin \varphi \right)+C=0$

здесь $\rho$ — полярный радиус, $\varphi$ — полярный угол.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Уравнение прямой

Свойства прямой в евклидовой геометрии

Общее уравнение прямой

Уравнение прямой по точке и нормальному вектору

Уравнение прямой с угловым коэффициентом

Уравнение прямой в отрезках на осях

Нормальное уравнение прямой

Уравнение прямой, проходящей через две заданные несовпадающие точки

Уравнение прямой по точке и направляющему вектору

Параметрические уравнения прямой

Уравнение прямой в полярных координатах