Числовые неравенства и их решение
Определение и формулы числовых неравенств
Число ![]() больше числа
больше числа ![]() , если разность
, если разность ![]() является положительным числом.
является положительным числом.
Число ![]() меньше числа
меньше числа ![]() , если разность
, если разность ![]() является отрицательным числом.
является отрицательным числом.
Если число ![]() больше числа
больше числа ![]() , то пишут
, то пишут ![]() , если число
, если число ![]() меньше числа
меньше числа ![]() , то пишут
, то пишут ![]() .
.
Для любых чисел ![]() справедливо только одно из соотношений:
справедливо только одно из соотношений:
![]()
Также для записи математических неравенств используют знаки ![]() (больше или равно) и
(больше или равно) и ![]() (меньше или равно).
(меньше или равно).
Знаки <, > называют знаками строгого неравенства, а знаки ![]() — знаками нестрогого неравенства.
— знаками нестрогого неравенства.
Основные свойства числовых неравенств
- Если
 и
и  , то
, то  (если
(если 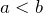 и
и 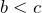 , то
, то  );
); - Если
 и
и  — любое число, то
— любое число, то 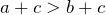 (если
(если 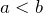 и
и  — любое число, то
— любое число, то 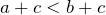 );
); - Если любое слагаемое перенести из одной части верного неравенства в другую, изменив при этом знак слагаемого на противоположный, то получим верное неравенство;
- Если
 и
и  — положительное число, то
— положительное число, то  , если
, если  и
и  — отрицательное число, то
— отрицательное число, то 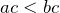 (если
(если 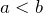 и
и  — положительное число, то
— положительное число, то 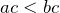 , если
, если 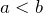 и
и  — отрицательное число, то
— отрицательное число, то  )
) - Если
 и
и  , то
, то 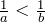 .
.
Операции с неравенствами
- Если
 и
и  , то
, то 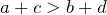 ;
; - Если
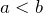 и
и 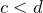 , то
, то 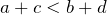 ;
; - Если
 и
и 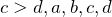 — положительные числа, то
— положительные числа, то  ;
; - Если
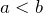 и
и 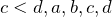 — положительные числа, то
— положительные числа, то 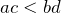 ;
; - Если
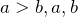 — положительные числа, то
— положительные числа, то  , где
, где 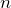 — натуральное число.
— натуральное число.
Примеры решения числовых неравенств
| Задание | Доказать, что |
| Доказательство | Очевидно, что справедливы следующие неравенства Что и требовалось доказать. |
| Задание | Известно, что |
| Решение | По условию |
| Ответ | Неравенство является верным |











