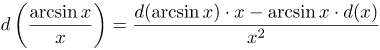Свойства дифференциалов

1. Дифференциал константы равен нулю:

$dC = 0\text{ },\text{ } C = \text{const}$

ПРИМЕР

$d(e^2) = 0$

2. Дифференциал суммы функций равен сумме дифференциалов слагаемых:

$d(u(x) + v(x)) = du(x) + dv(x)$

ПРИМЕР

$d(\ln x + 3^x) = d(\ln x) + d(3^x)$

Следствие. Если две функции отличаются на константу, то их дифференциалы равны:

$v(x) = u(x) + C \text{ } \Rightarrow \text{ } dv(x) = d(u(x) + C) = du(x)\text{ },\text{ } C = \text{const}$

3. Дифференциал произведения двух функций равен произведению дифференциала первой функции на вторую плюс первая функция на дифференциал второй:

$d(u(x) \cdot v(x)) = d(u(x)) \cdot v(x) + u(x) \cdot d(v(x))$

ПРИМЕР

$d(e^x \cdot \sin x) = d(e^x) \cdot \sin x + e^x \cdot d(\sin x)$

Следствие. Постоянный множитель можно выносить за знак дифференциала:

$d(Cu(x)) = Cdu(x)\text{ },\text{ } C = \text{const}$

4. Дифференциал частного двух функций $u(x)$ и $v(x)$ задается формулой:

$d \left( \frac{u(x)}{v(x)} \right) = \frac{du(x) \cdot v(x) - u(x) \cdot dv(x)}{(v(x))^2} \text{ },\text{ } v(x) \ne 0$

ПРИМЕР

5. Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной функции на дифференциал аргумента независимо от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Свойства дифференциалов