Производные высших порядков
![]()
Аналогично, если производная ![]() существует и дифференцируема, то можно найти третью производную рассматриваемой функции:
существует и дифференцируема, то можно найти третью производную рассматриваемой функции:
![]()
Таким образом, понятие производной ![]() -го порядка вводится индуктивно путем последовательного вычисления
-го порядка вводится индуктивно путем последовательного вычисления ![]() производных, начиная с производной первого порядка. Переход к производной следующего, более высокого порядка производится с помощью рекуррентной формулы:
производных, начиная с производной первого порядка. Переход к производной следующего, более высокого порядка производится с помощью рекуррентной формулы:
![]()
Замечание. Порядок производной, чтобы не путать с показателем степени, пишут в круглых скобках либо записывают римскими цифрами. Например, производная четвертого порядка
![]()
При нахождении производных высшего порядка используются следующие соотношения:
![]()
![]()
Примеры вычисления производных высших порядков
| Задание | Найти |
| Решение | Вычислим первую производную заданной функции:
Вторая производная есть производная от первой производной, то есть |
| Ответ |
| Задание | Найти |
| Решение | Для начала найдем несколько первых производных и постараемся установить закономерность:
Обобщая полученные результаты, делаем вывод, что |
| Ответ | 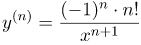 |






![Rendered by QuickLaTeX.com \[ y^{(n)} = \left( \frac{1}{x} \right)^{(n)} = \frac{(-1)^n \cdot n!}{x^{n + 1}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-be02842f2154772ce8bc2549dc13f8f0_l3.png)





