Производная тангенса
![Rendered by QuickLaTeX.com \[ \left( \text{tg} x \right)' = \frac{1}{\cos^{2} x} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-fd0efc0a5c38690818837c18fce61c3e_l3.png)
Эту формулу легко получить, зная производные синуса и косинуса:
![]()
а также формулу дифференцирования частного:
![]()
Согласно тригонометрическим формулам
![]()
Тогда
![]()
![]()
Примеры решения задач по теме «Производная тангенса»
| Задание | Найти производную функции |
| Решение | Искомая производная:
Перепишем функцию, стоящую под знаком производной, следующим образом: То есть функция представляем собой степенную функцию. Производная от такой функции находится по формуле: Так как основание степени представляет собой выражение более сложное, чем просто Производная тангенса равна единице деленной на косинус в квадрате, тогда |
| Ответ | 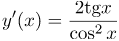 |
| Задание | Найти производную функции |
| Решение | Искомая производная
Согласно правилам дифференцирования, константа выносится за знак производной: Производную от тангенса находим по формуле: Но так как в нашем примере аргумент тангенса есть сложной функцией (выражение Константу 5 выносим за знак производной: Производная от независимой переменной |
| Ответ | 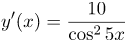 |











