Производная параметрической функции
![Rendered by QuickLaTeX.com \[ \begin{cases} x = x(t)\\ y = y(t) \end{cases} , \text{ } a \le t \le b \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e73c83ab15b015fabfea1e87b869d31d_l3.png)
В этом случае говорят, что функция ![]() задана параметрически.
задана параметрически.
Первая производная функции, заданной параметрически, задается следующей формулой:
![]()
Вторая производная ![]() функции, заданной параметрически, находится по формуле:
функции, заданной параметрически, находится по формуле:
![]()
Примеры вычисления производных параметрических функций
| Задание | Найти первую производную функции заданной параметрически
|
| Решение | Согласно формуле, нам надо найти производные функций Тогда искомая производная функции |
| Ответ |
| Задание | Найти вторую производную функции, заданной параметрически:
|
| Решение | Для того чтобы найти вторую производную Найдем производные Тогда первая производная Вторая производная то есть |
| Ответ | 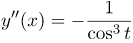 |






![Rendered by QuickLaTeX.com \[ \begin{cases} x = t - 2 \\ y = t^2 - 4 \end{cases} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d3b5ad929a6a982ae94083452eb9554d_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases} x = \sin t \\ y = \cos t \end{cases} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-79cad212919cec0ac92510b802fcd712_l3.png)





